一本书教你通关计组实验(上)
前言
我打算采用 Q & A 的方式编写前言,谁同意,谁反对?
Q:这是一本怎样的书?
A:如你所见,这是一本非官方的北航 6 系《计算机组成》课程通关指南。我希望学弟学妹们能够通过阅读这本书,以更小的负担、更高的效率,更轻松快乐地完成计组实验课程!
Q:为什么要写这本书?
A:这就要从我上大二的时候说起了。在刚进入 6 系时,我对很多计算机相关的知识完全没有任何了解,在学习计组课程时,面对着官方指导书中专业的术语和简洁的内容完全不知所措。最后也是在学习的过程中不断摸索,拜读了各位学长和同学的博客,才连滚带爬地完成了计组实验课程。我相信 6 系有很多同学和我的状态非常类似,于是在今天我选择回过头来,将我一年来艰难摸索出的知识用通俗易懂的语言写出来,帮助学弟学妹们少走弯路,通关计组实验课程!
Q:这本书有什么特点?
A:这本书最直观的特点或许就是篇幅特别长,在写作时我从不吝惜字数,经常是写这个部分的时候突然想到还应该讲一下那个部分,所以字数就像线面一样疯狂繁殖(摊手)。另外一个比较明显的特点就是文风比较诙谐幽默,毕竟又不是官方教程,篇幅还那么长,为了让大家能更开心地读下去,我充分利用了多年网上疯狂冲浪的经验,偶尔会玩一些梗,让大家开心开心,放轻松一点。
Q:创作这本书的历程是怎么样的?
A:这本书从 2025 年 3 月份开始创建文档,一直到开学前一天 9 月 7 号投入试读,历时半年左右。期间因为大二下学期各种压力都很大,鸽了相当长一段时间,所以前后的行文特点上可能有所区别,不过肯定的是全都是我一个人写的,也没有使用大模型代笔。(其实从文中玩的一些梗流行的时间就能大致推断出这一段是什么时候写的,笑)
Q:你的教学理念是什么样的?
A:在本书的写作中,我坚持以问题作为引导,围绕“如何使用”和“为何使用”两大主题进行写作,尽力帮助大家构建起整体的、连贯的认知思维。此外,我认为教学不能是空谈长篇大论的原理,这样虽然做到了严谨,但却陷入了大学教材普遍的“防自学”怪圈。相反,在本书的写作中,我用大量的文字带领大家在例子中学习,对极为晦涩且几乎没用的知识尽量回避,力争用通俗易懂的语言完成教程,希望大家能够一看就懂,一点就通!
Q:对于大量留白式的、鼓励学生探索的教程,你的看法如何?
A:可以预见的是,有人一定会批评我把所有东西都直接讲出来,不给学生探索的空间,是一种扼杀同学积极性的填鸭式教学。然而我并不赞同此种观点。事实上,我以前也是一个宁可自己死磕,也不愿意求助他人的人,我也曾经认为这是一个很好的锻炼思维的过程。然而在 6 系大二一年的毒打中,我逐渐体会到一个道理:我们的时间是短暂和珍贵的,有很多问题自己思考一周,不如别人一句话点透其中的道理,只要对方能够把问题讲清楚,获得的收益不比自己探索更差,还大大提高了解决问题的效率,我认为实在是大有裨益。在写作的过程中,我也经常会引导同学们思考,不过不是以留白的形式,而是在短暂的思考之后继续讲解清楚。有些内容根本不是初学者能够理解的,过度思考毫无意义,浅尝辄止即可。
Q:使用这本书有什么注意事项吗?
A:禁止食用(x)其实没有什么特别的注意事项,你甚至可以当小说来读,轻松愉快就好。如果想亲自动手体验一下书中的电路和代码的话,我将书中的一些电路和代码打包放在了北航云盘里:https://bhpan.buaa.edu.cn/link/AACB2D43EFCB9C438EA2D9539686E34943
(文件夹名:cocheckmate ,有效期限:永久有效,提取码:COCM ),可以下载下来玩一玩。
Q:对于书中可能出现的问题,如何及时反馈?
A:如果你对书中的内容有疑问,包括但不限于讲述错误、没讲清楚、根本没讲等问题,还请及时发邮件到我的北航邮箱:blumaha@buaa.edu.cn ,我将在两天之内给出回复,如果两天没回可能是看完之后忘了,可以再给我发邮件。我将在下册的结尾予以致谢,感谢各位为本书做出的贡献!
Q:最后,有什么想对学弟学妹们说的?
A:同学们,计组实验是你们来到 6 系的第一大关,它看似非常可怕,但我愿与你们一同闯过层层难关,帮助你们取得最终的胜利。希望你们在学期末通过最后一次上机时,能够淡然地回望来时的路,像老朋友一样与这门课程挥手作别,勇敢自信地奔向下一个挑战!
目录
第一章:Logisim 与数字电路
1.1 初识 Logisim
1.2 输入、输出、门电路
1.3 调整位宽:从一位到多位
1.4 复杂的组合逻辑:数学运算与译码器
1.5 时序电路:从锁存器、触发器,到寄存器
1.6 寄存器后日谈
1.7 本章结语:再见,Logisim!
第二章:汇编语言 MIPS
2.1 汇编语言与 MIPS 简介
2.2 MARS 简介
2.3 MIPS 语法初步
2.4 MIPS 编程实战
2.5 MIPS 机器码
2.6 本章结语:再见,MIPS!
第三章:硬件语言 Verilog
3.1 硬件语言简介
3.2 ISE 简介
3.3 Verilog 语法初步:常量、变量与运算
3.4 Verilog 语法初步:组合逻辑与时序逻辑
3.5 Verilog 编程实战
3.6 有限状态机
3.7 本章结语:再见,Verilog!
第一章:Logisim 与数字电路
1.1 初识 Logisim
终于,你将要迈出计组实验的第一步了!不过不要害怕,这本教程会全程一直陪伴着你,帮你走完这一段艰难又收获满满的旅途!首先,相信你已经下载好了我们必要的软件 Logisim (如果还没有,请先参照官方指导书),作为三款软件中最为拟人的一部(大概吧),Logisim 的界面十分简洁,非常便于我们理解和学习。
【打开Logisim】
打开 Logisim ( jar 文件和 exe 文件均可,没有区别),我们可以看到如下界面:
【创建、打开Logisim文件】
我们先不需要学习任务栏中全部的内容,毕竟我们的旅途才刚刚开始嘛!第一步,我们打开 File 任务栏,使用 New 创建一个新的文件,使用 Save / Save As 保存这个文件,别忘了将它放在一个比较正式的文件夹里,这里将会保存你整个学期所有的 Logisim 工程,当你在学期结束时回头看这个文件夹的时候,你一定会收获满满的成就感!
OK ,现在你可以退出 Logisim ,重进 Logisim ,再次打开 File 任务栏,使用 Open 打开你刚才创建的文件(其实在文件夹中直接双击这个文件也可以打开),你已经掌握了最基本的文件操作方法了!
【调整画面比例】
虽然这个时候说有点早,但是还是想提醒你一下:在界面的左下角有一个 100% ,这是当前视图的缩放比例,如果你真正开始上手操作,就会发现这个比例有点太小了,为了避免目害,你可以顺着这个 100% 往右找,看到旁边的上下箭头了吗?点击它们就可以调整视图的比例!不瞒你说,许多人到课程结束都没发现过这个按钮(悲)!
1.2 输入、输出、门电路
我们知道,大多数学校的计算机学院都有一门课程,名字叫作数字电路,这是学习计算机不可省略的一步。然而我们就恰恰没有这门课程,但学习 Logisim 的过程,其实就是在学习数字电路。
【数字电路】
那么,什么是数字电路呢?在我看来,与其说这是一种电学,不如说这是一种数学,是 0 和 1 组成的逻辑运算的具象化。相信各位在去年已经学习过了离散数学的数理逻辑部分,数字电路要做的其实就是将这些表达式以“电路”形式呈现出来,将它们可视化地运行。
如果你是 Minecraft 牢玩家,对红石系统有一定了解的话,你会发现其实红石系统就是比较简单的数字电路,拉杆就是输入,红石灯就是输出,红石火把则是常数 1 和非门,通过不同的组合,我们就可以打造出各种门电路。事实上,和仅供娱乐的游戏相比,Logisim 里提供了更加丰富的数字电路元件,不需要我们自己去用与或非门一点点拼出来,有着更多可能等待我们去探索!
【输入、输出、电路的运行】
接下来我们回到学习中,请关注模块中 Wiring 和 Gates 部分,它们就是我们本节课的主角。点击界面左上方的正方形按钮(或 Wiring 中的 Pin ),再点击工作区的任意位置,我们可以放下一个输入端;同样,点击界面左上方的圆形按钮,我们能够放置一个输出端。使用左键拖动,将输入端的右侧和输出端的左侧连接起来,我们就完成了数字电路中的 “Hello, World!” !点击左上角的小手,切换到调试模式,点击输入端切换其 0 和 1 的状态,感受输出端的变化吧!
(注:图中的“调试模式”和“编辑模式”并非官方翻译方法,本书中将保持这种翻译方法,如有官方翻译,以官方翻译为准)
【Logisim中的快捷键】
如果我们需要解除两个元件之间的连接,只需要将鼠标放在二者连线的一端,沿着这段导线拖动即可。和我们熟悉的操作一样,使用左键在空白区域拖动框选之后,使用 ctrl + X 可以进行剪切操作,使用 ctrl + C 复制,使用 ctrl + V 粘贴,使用 crtl + D 复制并粘贴,使用 ctrl + A 全选,使用 crtl + Z 撤回。( Logisim 貌似不能取消撤回,请谨慎使用 ctrl + Z )另外还有更多的快捷键,可以将鼠标悬停在选项栏上查看。
【逻辑门】
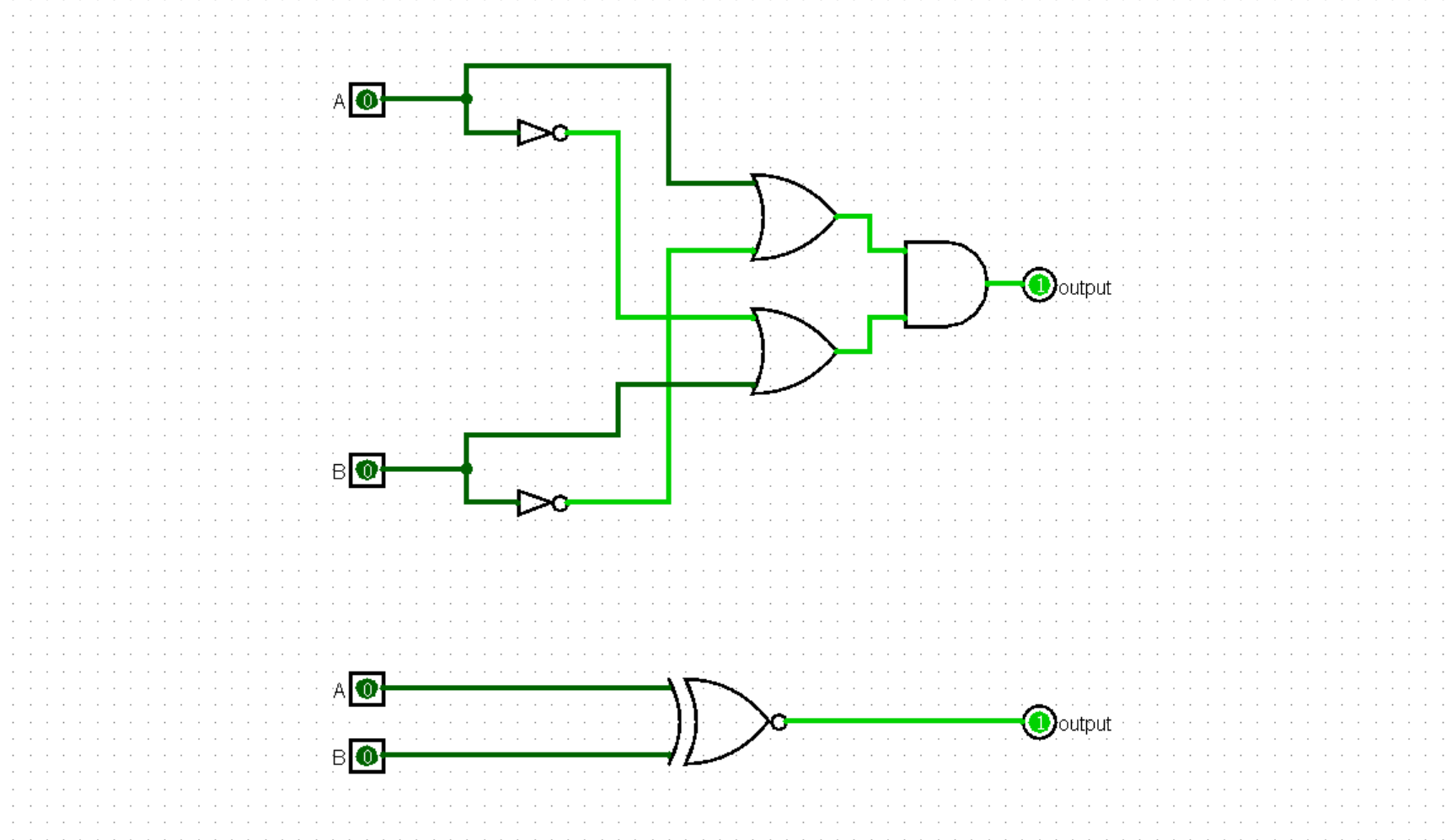
相信读到这里的绝大多数同学都已经学过了离散数学,在 Logisim 中,我们可以将离散数学中学到的逻辑运算具象化。在 Gates 中有着丰富的逻辑门,使用它们可以进行逻辑运算,下面你可以尝试使用它们它们表示出一个逻辑表达式,例如下面这个:
$$ output = (\lnot A \lor B) \land (\lnot B \lor A) $$
这是互蕴含的表达式,你可以再放一个同或门,看看两者输出是否相同!
【元件的属性设置】
相信你已经发现了,我们在摆放逻辑门时,默认摆放的是五输入的逻辑门,为了将其改为二输入,我们进入编辑模式,左键单击元件,即可在左侧对其进行设置。在下面这个网站可以查询所有元件的所有属性,在认识元件之前读一读它的介绍,或许能够掌握它们更多有趣的变化:
https://cburch.com/logisim/docs/2.6.0/en/libs/gates/basic.html
(美中不足的是,这个网站是全英文的,如果在阅读上有困难,可以在 Logisim 上自己修改属性试一下,看看会发生什么变化。我保证,这不会把你自己的 Logisim 玩坏的!)
【奇校验、偶校验】
在 Gates 中有两种我们没有见过的元件,即 Odd Parity(奇校验)和 Even Parity(偶校验),尝试放置一个二输入的奇校验或偶校验,看看它们的输出如何?
或许你已经发现了,二输入的奇校验和异或门完全相同,二输入的偶校验和同或门完全相同。然而我们用十二指肠想,两者也不可能是完全相同的,奇偶校验和异同或门的差别其实体现在多输入上。
【多输入】
在最开始我们就发现了,逻辑门可以有不止两个输入(默认是五个),其实多输入表示的含义很简单,在大多数逻辑门中,多输入表示的都是多个输入进行连续运算,比如一个输入为 A B C D E(均为 1 位)的电路,通过一个默认五输入的与门,输出为 output ,则它们的关系为:
$$ output = A \land B \land C \land D \land E $$
然而在异同或门中,事情似乎发生了一些变化。试着创建一个五输入的异或门电路,观察一下输出如何?
我们惊奇地发现,异或门输出为 1 当且仅当:有且仅有一个输入为 1 ;同或门输出为 0 当且仅当:有且仅有一个输入为 1 。也就是当值为 1 的输入个数是一个大于 1 的奇数时(如 3、5、7 等),异同或门的输出和我们想象中的并不一致!这非常奇怪,完全不符合我们的直觉,然而底层代码是这样写的,我也没办法(摊手)。
| 输入为 1 的个数 | 异或门输出 | 同或门输出 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
| 2 | 0 | 1 |
| 3 | 0 | 1 |
| 4 | 0 | 1 |
| 5 | 0 | 1 |
然而,反转又来了,请你再试一下刚才提到了奇偶校验,用奇校验替换上述电路中的异或门,用偶校验替换上述电路中的同或门,看这次的输出如何?
有趣的是,奇偶校验的性质正和我们想象中的“异同或门”完全相同:奇校验输出为 1 当且仅当:有奇数个输入为 1 ;偶校验输出为 1 当且仅当:有偶数个输入为 1 。原来奇偶校验才是真·异同或门!
| 输入为 1 的个数 | 奇校验输出 | 偶校验输出 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
| 2 | 0 | 1 |
| 3 | 1 | 0 |
| 4 | 0 | 1 |
| 5 | 1 | 0 |
1.3 调整位宽:从一位到多位
在刚才的学习中,我们介绍了门电路的用法,虽然引进了多输入,但我们的自变量(输入)却依然只有 0 和 1 两种可能,这在实际应用中显然是不够的。于是,我们开始拓宽输入的位宽,进行更加复杂的运算!
【位宽】
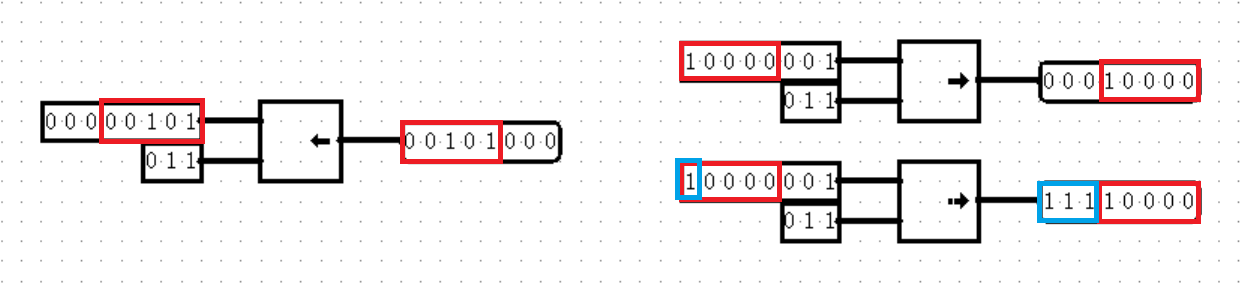
在输入的属性中,有一项是 Data Bits ,这就是设置位宽之处。我们先搭建一个最简单的二输入与门电路,紧接着调整其中一个输入的位宽(例如为 4 ),然后……出现错误了。橙色的错误代表着位宽不一致,顺着图中标橙的导线看去,我们发现原来是导线两端的位宽出现了不一致:输入是 4 位,而与门是 1 位。这说明逻辑门也是有位宽的!
事实上,几乎所有的元件都有位宽,有些元件的输入端和输出端甚至有着不同的位宽(例如我们将要讲到的 Bit Extender ),所以在接下来的实验中,我们一定要时刻注意位宽问题。得益于 Logisim 没有隐式的位宽转换,只要位宽不同就会直接报错,我们只需要在报错时及时修改即可,然而之后要学习的 Verilog 语言会让你体会到位宽的背刺的(笑)。
在修改完一串位宽不一致的问题之后,我们的两个输入、与门和输出都已经变成了 4 位,现在我们可以进入调试模式看一下输入与输出之间有着怎样的关系了。
通过观察我们不难发现,对于上节中讲过的可以进行一位逻辑运算的逻辑门,多位运算其实就是将每一位拆开分别运算,最后按原来的位置合在一起,和 C 语言中的位运算 & | ^ 等是完全一致的。什么嘛,原来多位运算也没有那么难嘛~
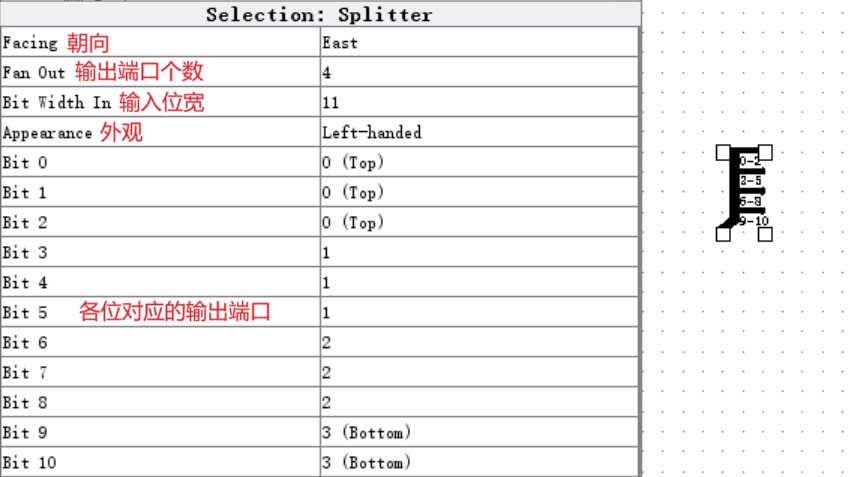
【Splitter、位数的定义】
接下来,我们来继续认识一些新的元件。就先从 Wiring 这部分开始吧!
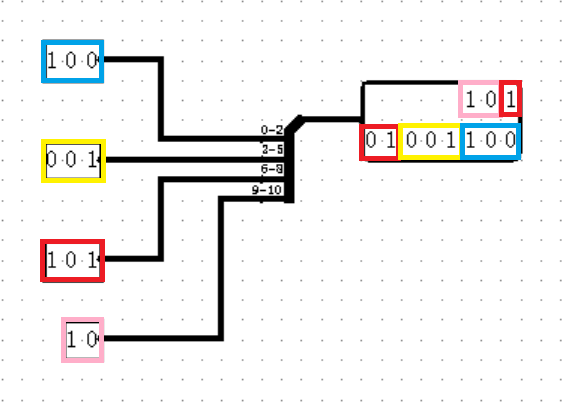
Splitter 是一个非常重量级的元件,将会撑起之后实验的半壁江山。见字知意,它的作用就是将一个多位宽的输入分割成多个任意位宽的输出(其实不止如此)。我们放置一个 Splitter ,它的属性参数如下:
通过属性参数的组合,我们可以将任意位宽的输入切割成任意份任意位宽的输出,实在是太方便了!然而,我们千万千万千万千万要注意位数的对应!!!我们对位数的定义和 C 语言的位运算是一致的,对于一个 11 位的数据 abcdefghijk(其中所有的字母均代表 0 或 1),它的最高位是第 10 位的 a ,最低位是第 0 位的 k ,这一点请千万牢记,左高右低,最低位为第 0 位,我们在计组课程中提到的所有位数都是如此定义的!
此外,虽然 Logisim绝大多数元件都不支持输入端和输出端倒置,但 Splitter 却是个确确实实的例外!这也就意味着……它既可以将一个大位宽的值分割成多个小位宽,还能将多个小位宽的值合并成一整个大位宽!据说还是有很多人没有发现这个巧妙的用法,看了我的教程,可不许再说你不会这么用了!(骄傲)
(如果你仔细观察就可以发现,上图中有一个很奇葩的问题,Logisim 默认字体中的数字 3 长得和数字 2 几乎一模一样,这不可疑吗?)
【Wiring中的其它元件:Probe】
在一位的电路中,我们能够很容易看出电路中哪部分的值为 0 ,哪部分的值为 1 ,这得益于两种取值对应的导线颜色是不同的:如同人体的动静脉血一样,0 是暗绿色,而 1 是亮绿色。
然而,在多位电路中,无论每位取值如何,导线都只有黑色一种颜色(没连错的情况下),那么我们应该如何知道此时此刻通过导线的数值呢?于是有了 Probe 。将它连接在导线上,甚至不需要设置位宽,即可以实时显示当前通过导线的数据,用于调试非常方便!
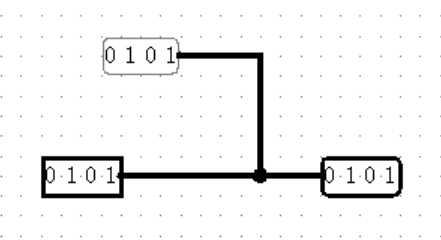
【Wiring中的其它元件:Tunnel】
另一个为方便而诞生的工具是 Tunnel ,顾名思义,它承担着隧道的作用,名字相同的两个 Tunnel 之间在我们看不见的地方相互连接,无论相隔多远,不需要受到连线的限制!
【Wiring中的其它元件:Constant】
接下来到场的是两种新的输入方式:Constant 和 Clock !我们在连接电路时,经常会遇到需要输入一个常量的情况,这种时候如果使用 Input 作为输入是不可行的:一方面,它的值是固定不住的,即使我们手动设置好了初始值,关闭文件再次打开之后又会归零;另一方面,它也会使元件的外观发生改变,会导致元件多出一个输入端。所以这时不动如山的 Constant 登场了,和 Input 的用法完全相同,它的值永远固定,除非你手动更改它!
【Wiring中的其它元件:Clock】
如果你在界面上放下一个 Clock ,你会发现它和一位的 Input 在使用上没有任何区别,事实上确实如此。但是请看左上角选项栏中的 Simulation 一项,这里隐藏着 Clock 的全部特殊用法。
在 Simulation 中选择 Ticks Enabled ,你会发现 Clock 开始自己动起来了!是的,现在的 Clock 正以一秒钟为单位不断翻转着自己的输出,如同摆钟一样。在 Tick Frequency 中,我们可以调节 Clock 翻转的周期,让它翻转得更快一些吧!
(PS: 不要碰上面那个 Simulation Enabled,有很多人以为自己的 Logisim 卡死了,实际上是不小心把这个开关关掉了(笑))
事实上,我们一般不拿 Clock 当作数据的输入端,它的存在是服务于时序逻辑电路中的使能端,当然这是很后面的事情了,我们暂时只知道有这么个东西就可以了,千万不要忘记它哦~
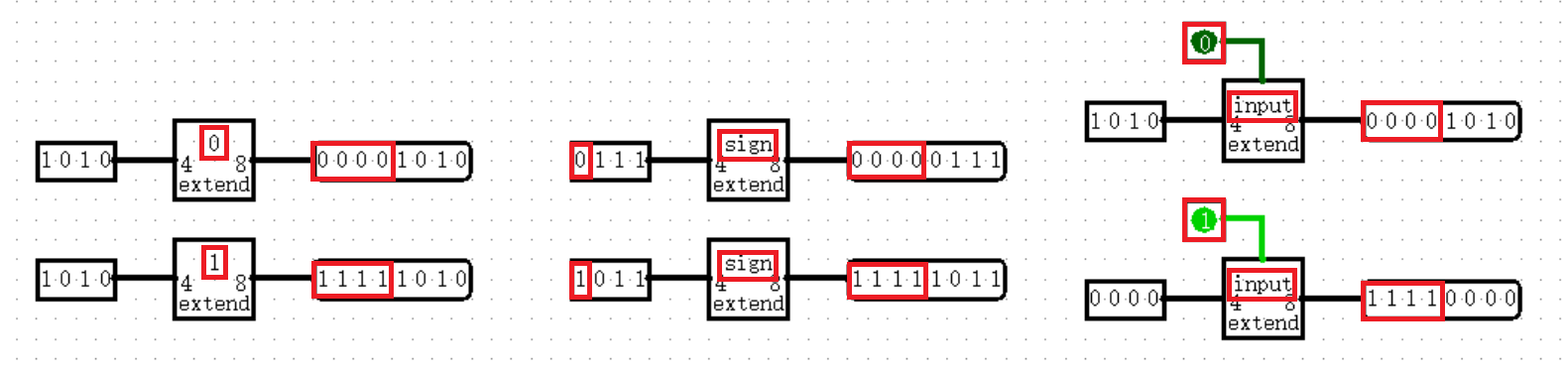
【Wiring中的其它元件:Bit Extender】
当你需要改变一个数据的位宽时,目前你肯定会想到用 Splitter 进行拼接,但是这样会产生非常多的常量(Constant),这既不方便也不优雅,于是我们又有了 Bit Extender ,它可以非常方便地拓展位宽,多种模式,任君选择!
在属性参数中,我们可以设置 Extension Type ,即扩展模式,如果选择 Zero 或 One ,则会将高于输入位数的部分全部置 0 或置 1 ;如果选择 Sign ,则会根据输入的最高位决定高位置 0 还是置 1 ;如果选择 Input ,Bit Extender 的上方会出现一个接口,在这里连入一个一位的输入,由它来决定高位置 0 还是置 1 ,灵活性非常强!
1.4 复杂的组合逻辑:数学运算与译码器
其实到这里,我们已经学习了相当多的知识,然而当我告诉你,接下来的几节才是 Logisim 这部分的重量级选手,你会怎么想?
【Arithmetic中的基础元件】
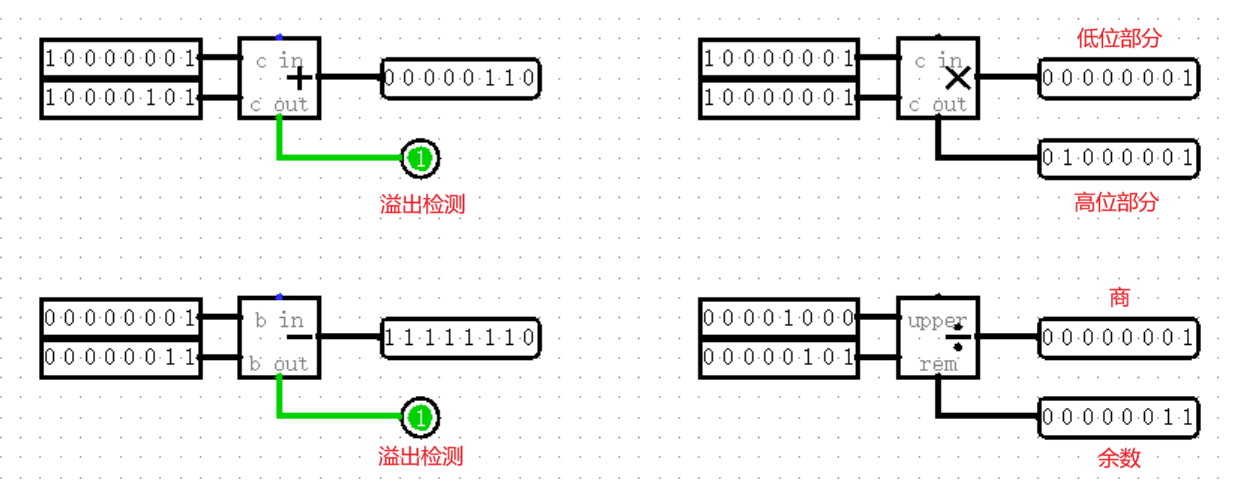
Logisim 非常好心地为我们内置了四则运算的模块,这样我们就不需要自己写全加器和乘法器了!(不过你早晚会在作业的练习题中见到它们的)只需要打开 Arithmetic 文件夹,你就可以轻松使用它们!
值得一提的是,每个模块下面都额外带有一个输出,这些输出意义各不相同,但每个都十分重要(其实上面也有,只是完全没太大用)。
加减法模块下方的输出为溢出检测,当计算发生溢出时,模块本身不会报错,只是会单纯地丢掉溢出的最高位,你也可以理解为溢出的最高位被扔到了下面的输出,事实上,只要用 Splitter 将二者接到一起,你就可以得到一个完整的结果。
为了使输入输出位宽相同,乘法的结果被分为了两部分,较低的一半被分配至正常的输出端,而较高的一半则由下方的额外输出承担;同样,除法的商位于正常输出端,余数位于下方额外输出端。这种设计会在 MIPS 语言中再次出现,回过头来看真的是好经典啊~
【Arithmetic: Negator】
或许你以为 Negator 只是一个简单的取反器,如同 C 语言的 ~ 符号一样将每位取反,你就真的是图样图森破了!实际上,Negator 的运行原理是这样的:
是的,它有一种很奇怪的运行方式:首先找到位于最低位的 1 ,然后将比这个 1 更高位的所有位数取反。这样设计是为什么呢?说实话我也不太清楚。
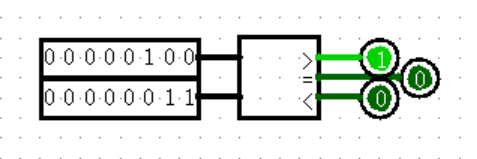
【Arithmetic: Comparator】
Comparator 真的很纯粹,输入两个值,然后返回一位的比较结果,就这么简单。实际上你甚至不需要在右端连上三个输出,只取一个你想要的即可。
然而醒醒,这不是数学,这是数字电路!二进制让比较变得不纯粹了,在二进制的世界里,正数和负数的界限不再分明,用人话来说,就是你需要确定你所输入的数据究竟是不是有符号的,这在以后所有的比较大小中都尤为重要!!!Logisim 中的 Comparator 默认是有符号比较,也就是会出现下面这种情况:
根据补码的原理,这里的全 1 其实代表的是 -1 ,所以上面大于下面也是显然了。如果想无符号比较怎么办?点一下这个模块,在左边调一下属性参数就好了。
【Arithmetic: Shifter】
Shifter 其实就是移位器,道理很简单,和 C 语言的 << 符号和 >> 符号几乎完全相同,不过因为移位的过程中必然会产生空缺的位置,所以还是要注意置 0 还是置 1 的问题。实际上左移是没什么问题的,在左移的过程中,高位被挤掉,低位补充上 0 即可,然而右移就要分两种情况讨论了:一种情况下,数据右移后低位被挤掉,空缺出的高位上正常补 0 ,这就是逻辑右移(Logical Right);另一种情况下,数据右移后低位被挤掉,空缺出的高位上则要根据原数据的最高位决定补 0 还是补 1 ,这就是算术右移(Arithmetic Right)。真够复杂,不是吗?以后有的是让你抓狂的。
其实在属性参数列表中,你还能看到两种位移:循环左移(Rotate Left)和循环右移(Rotate Right),它们没什么坑点,但也不常用,无非就是原本被挤掉的位数,会从另一端再回来罢了,所谓循环。
【Arithmetic: Bit Adder】
一个会让你觉得“怎么还会有这种元件”的元件,存在感实在很低,考试的时候有很多人都想不起来用它。它的作用就是统计输入端每位上总共有多少个 1 ,没有任何注意事项,真是滑稽。
【Arithmetic: Bit Finder】
Bit Finder 的作用是寻找,至于寻找什么,那要你说了算。它提供四种属性参数,分别是找到 最高位 / 最低位 的 0 / 1 ,并输出它们所在的位数。
发现这其中 bug 了吗?如果你发现了,说明你的神经开始敏锐起来了!如果输入中根本没有我要找的 0 或 1 ,应该输出什么呢?好像无论输出什么都会和某些结果重合,于是它的下方出现了额外的一位输出,表示是否找到了这样的 0 或 1 。
顺带一提,如果没找到的话,右侧的输出固定为 0 。
到此为止,我们已经讲解完 Arithmetic 中所有的元件了!所有的元件在我们的实验中都有用处,真的是一件很不容易的事情。有了 Arithmetic 中的工具,我们就可以进行一些复杂的运算了。记住它们,用好它们,才能在以后的题目中找到更简单的解法!
一刻也没有为 Arithmetic 结束感到悲哀,接下来到场的是:
【Plexers: Multiplexer】
大名鼎鼎的 MUX 本尊,学名 多路选择器 。说起来其实很简单,但是总是把人搞得晕头转向。左侧输入多个数据,并从上往下从 0 开始编号,下侧输入一个编号进行选择,右侧仅输出下侧编号所对应的那个数据。有点像从数组中取一个数据,不是吗?
需要注意的是,MUX 的左侧输入位宽与右侧输入位宽有直接关系(相等),下侧输入位宽与左侧输入个数有直接关系(2的幂次),而前两者和后两者在位宽大小上没有任何关系。
此外,你也许注意到下侧还有另外一个接口,那个是 MUX 的使能端,然而如果不接任何导线(称为悬空态)的话,默认为开启使能,一般我们都不会考虑关闭 MUX ,所以这个接口也是常年空接,你也可以通过调整属性参数直接把这个碍眼的接口消灭掉。
这个元件在以后我们会经常用到,因为它几乎是实现分支判断的不二之选,当它的左侧输入端只有两个数据时,下侧输入端就只有 0 和 1 两种选择,配合万能的 Comparator ,就可以实现 if 一样的效果(当然也可以说更像三目运算符 ? : )。
【Plexers: Demultiplexer】
和 MUX 正好相反,DMX 是一输入多输出,看起来几乎就是镜像的 MUX ,以至于我都懒得在这张图片上 P 图做注解。
然而,这种时候大概率会有个转折,警惕性告诉我们,当输出多于输入的时候我们一定要想一想,多出来的输出是哪来的,竟然是凭空变出来的!也就是说,除了被选中的输出来自输入,其它的输出 0 不来自任何输入,是我们人为规定出来的,这也就导致了它们可能会对我们的电路造成干扰,这在我们搭建 CPU 的 GRF (寄存器堆)部分时会产生致命错误,在每个周期都将其余的所有寄存器覆盖为 0 ,这时候我们需要调整 DMX 的属性参数,将 Three-state? 参数改为 Yes 即可,此时其它输出默认为 x ,不会对后续产生影响。
现在讲这么多感觉还是有点多了,感觉作为初学者你可能也听不太懂,不过请记住这个位置,当你真的在搭 CPU 时翻车了,不要忘了回到这里看看,那时你会有更多的收获!
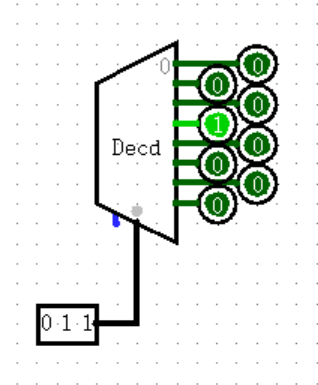
【Plexers: Decorder】
这位更是声名远扬的 译码器 本尊,计组理论常客,每年期末必考一道大题的东西。作用是将下方的输入转换为一位的“独热码”(One-Hot Encoding),有点像输入端固定为一位 1 的 DMX 。
下图所示的就是我们非常常见的 3-8 译码器,它实现了三位二进制码向八位独热码的转化。Logisim 貌似只支持单向转化,而在理论课中,译码器是可以双向互相转化的,能够实现极为复杂的效果,对于我这种理论不太好的选手还是挺难的。
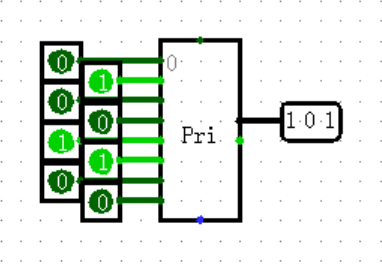
【Plexers: Priority Encoder】
优先编码器,一种另类的 MUX ,它的特点就是所有输入不再“平等”,而是根据自己的位置有着“优先级”,位置越靠下(下标越大)优先级越大,当多个输入同时亮起时,右侧只输出最靠下的输入的位置。
其实并没有什么存在感,本来不打算讲,结果突然想起以前貌似考过,于是小谈一下。问题在于它并非是不可替代的,有一种很简单的结构也可以快速实现这个功能,是什么呢?
(答案是 Splitter 将所有位合在一起后再 Bit Finder ,你猜对了吗)
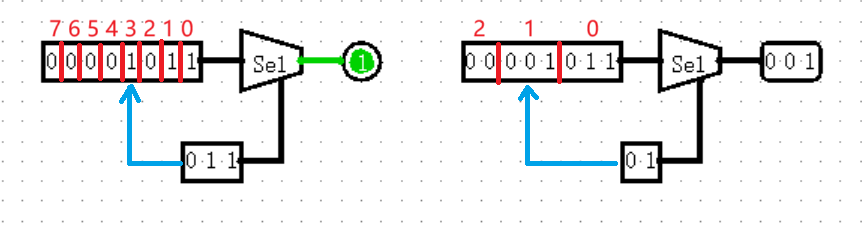
【Plexers: Bit Selector】
Bit Selector 的作用是根据输出位宽将左侧输入分成等宽的部分,再以下侧输入为序号,从低位向高位输出对应的字段输出,实际上相当于 Splitter 加上 MUX 进行分选。
我猜到你一定会问,如右图所示的情况有可能会取到左侧输入的外面,这个时候应该怎么办?事实上,和以往既有高位补 0 又有高位补 1 的情况不同,Bit Selector 的策略是高位一律补 0 ,没有其他选择。
到此为止,我们的本节课也该告一段落了。这节课的主要内容就是认识新的元件,这些元件看似简单,实则已经非常完备,配合我们下节将会讲到的寄存器,已经可以实现极为复杂的系统,甚至是 CPU 。比起理解更加不容易的是学会运用,在以后的 Logisim 上机考试中,我们是否能够根据需求反推出需要哪些元件,这也是需要修炼才能取得的成果。加油,我相信你可以的!
1.5 时序电路:从锁存器、触发器,到寄存器
目前为止,我们学习的所有内容都是“组合逻辑”,也就是将输入和元件进行组合,通过一系列运算得出输出。然而,我们虽然能够进行比较复杂的计算,但是还缺少了非常重要的一环,那就是存储。现在,我们要让我们的电路“动起来”,通过一步一步的构造,逐渐实现最基本的存储元器件 —— 寄存器。
【SR锁存器】
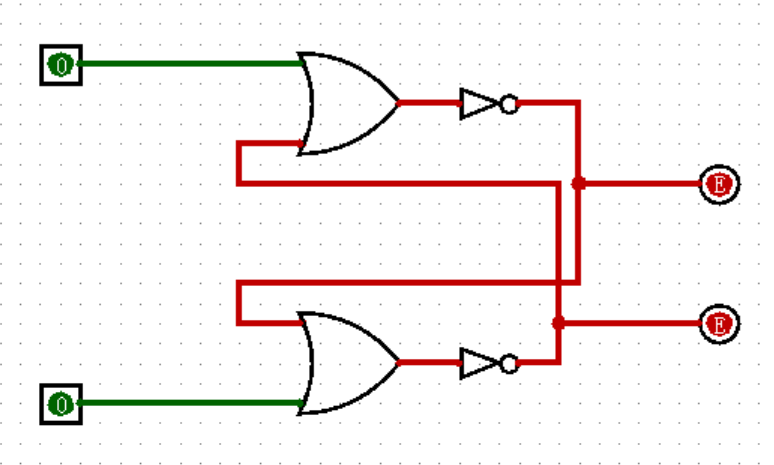
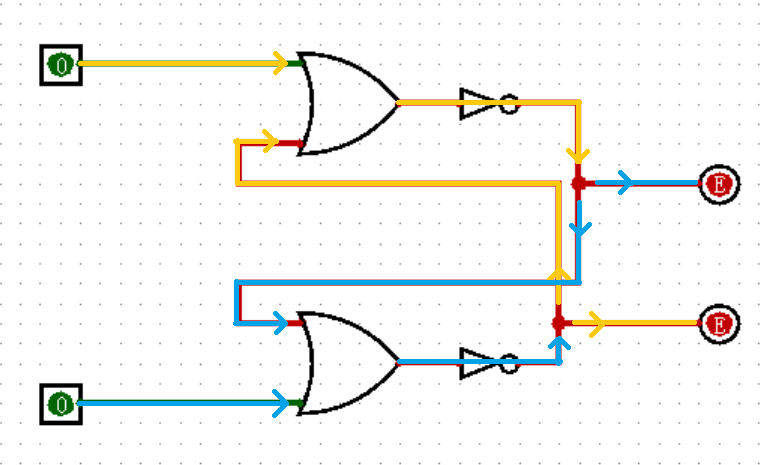
接下来,我将要向你介绍一个颠覆你之前所有认知,为你打开新世界大门的神奇电路:SR 锁存器(SR Latch)。
请像下图一样,在 Logisim 中连出这个电路:
图中出现了红色,它代表的是输出出现了冲突,无论输出 0 还是 1 都有可能。这种报错也经常出现在将两个输入不经过任何元件,同时直接连接到同一个输出上,当两个输入的数值不同的时候(比如一个是 0 ,一个是 1 ),输出就会变为红色。Minecraft 玩家应该格外注意这一点,如果想实现和游戏里一样的效果,必须使用或门。
回到正题,其实这个电路并没有错误,你可以试着改变一下两个输入的值,你就会发现红色的报错已经消失了!这是为什么呢?或者说,你真的能看懂这个电路吗?尝试一下吧!
如上图所示,上面的输出由两个部分经过或非门(或门后面接非门)构成,其中一个部分是上面的输入,另一个部分是下面的输出;同时下面的输出又由下面的输入和上面的输出经过或非门构成。
于是就形成了一个奇怪的现象:上面的输出控制着下面的输出,而下面的输出又控制着上面的输出,似乎形成了一个“衔尾蛇”,这也是电路最开始出现红色报错的原因。然而,为什么经过赋值之后,电路就能够成功跑起来了呢?我觉得用齿轮来比喻更加合适:我们小学二年级就学过,如果一个循环的齿轮组有偶数个齿轮,那么它就可以旋转,而如果有奇数个齿轮就会卡住,向任何一个方向都无法旋转。这个电路也是一样,只要形成巧妙的平衡,确保不出现“自相矛盾”的情况,就可以自由活动了!
比如观察输入为上 1 下 0 的情况,此时无论另一端输入如何,上面的或门输出一定为 1 ,于是上面的或非门输出为 0 ,上面的输出为 0 ,于是下方或门的两个输入为来自上方输出的 0 和来自下方输入的 0 ,所以下面的或门输出为 0 ,下面的或非门输出为 1 ,下方的输出为 1 。这就形成了一种固定的可能,而不会出现红色的报错!当然,由于这个电路是对称的,所以上 0 下 1 的情况也是同理。
接着,我们再观察输入为上 0 下 0 的情况,此时你的输出是上 0 下 1 还是上 1 下 0 ?如果你是在和你的好盆友一起边做实验遍看这本教程,当你们得出完全不同的输出时,不要着急开始一场大战,因为两种情况都是正确的!这实际上取决于你们是如何操作的。这不可疑吗?
如果你像刚才那样仔细分析两种输出,就会发现这两种情况都是成立的,区别实际上在于你是由上 0 下 1 的输入关闭了下面的 1 ,还是由上 1 下 0 的输入关闭了上面的 1 得到的上 0 下 0 的输入。用这两种情况再试一下?这就是锁存器的魅力时刻。
于是,经过一番长久的研究,设上下两个输入分别为 S 和 R ,上下两个输出分别为 Q 和 Q’ ,我们就可以用真值表总结出 SR 锁存器的所有情况:
| S | R | Q | Q’ |
|---|---|---|---|
| 0 | 0 | 和上一状态相同 | 和上一状态相同 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
看到这里,你一定会有疑问,为什么至今为止,我们好像都在刻意回避 S = 1 且 R = 1 这种情况。如果你真的去动手做了这个实验,你就会发现这种情况完全成立,两个输出都为 0 ,而且也不会出现因上一状态不同而输出不同结果的方法。
但是我们接下来就会知道,SR 锁存器的诞生是有它的使命的,创造它的人希望两个输出 Q 和 Q’ 永远输出两个相反的值(从它们的名字就可以看出来),于是输入全为 1 这种“不合群”的情况就被残忍地判决为了“非法”的情况,事实上,它完全不会导致你的电路出现任何 bug 。(悲)
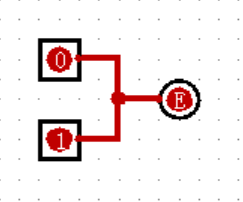
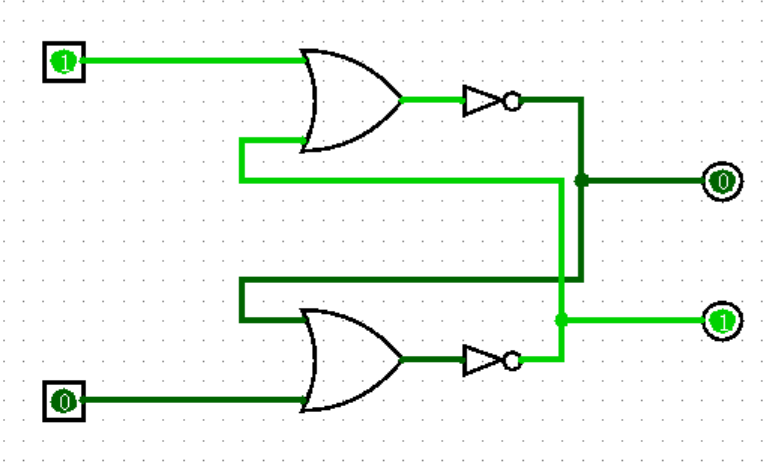
【D锁存器】
D 锁存器(D Latch)其实只是 SR 锁存器的一种特殊形式,不过它才是我们接下来故事的主角。将 SR 锁存器左侧的两个输入合并为一个,并在下面的一端加上一个非门,就形成了 D 锁存器,实际上也就是只有上 0 下 1 和上 1 下 0 两种输入的 SR 锁存器:
D 锁存器的逻辑非常简单,设输入端为 D ,上下两个输出依然为 Q 和 Q’ ,则 D 锁存器的真值表如下:
| D | Q | Q’ |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 0 | 1 |
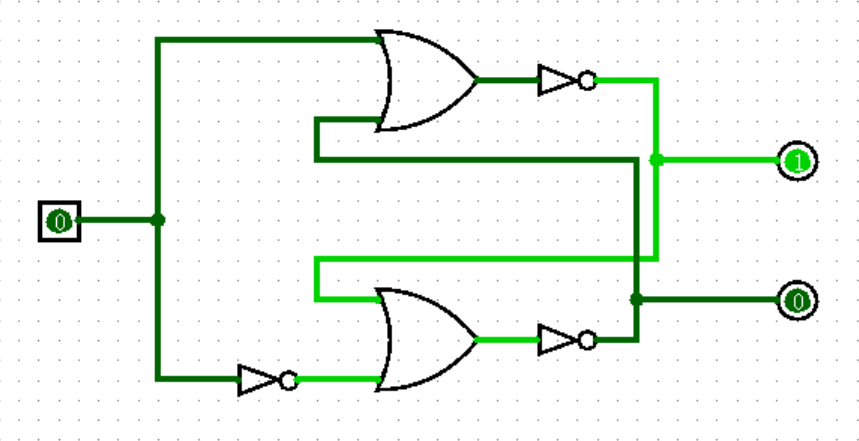
【带使能的SR锁存器和D锁存器】
现在,我们在 SR 锁存器和 D 锁存器的输入端都加上一个使能端:
其实非常好理解,当使能端为 1 时,带使能端的锁存器与不带使能端的锁存器相比,二者没有任何区别;而当使能端为 0 时,锁存器的输入被强制固定为两个 0 ,此时根据我们之前的分析,输出端会保持不变,无论输入端如何变化。( D 锁存器也是同样,别忘了它其实就是一种 SR 锁存器!)
看起来还是很好理解?记住这个带使能端的D锁存器(Gated D Latch),接下来我们要起飞了!
【模块化】
等一下,我们现在还不能起飞!工欲善其事,必先利其器。在此之前,我们还需要了解一下 Logisim 的新用法!
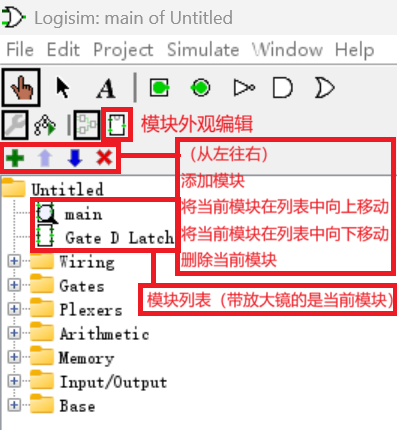
在接下来的实验中,我们的电路中经常会出现大量重复的部分,又或者是只需要暴露接口的集成度较高的部分。和写代码的时候需要定义函数的道理完全相同,我们在 Logisim 中也需要这样的“函数”,将一部分电路集成到一个模块中,调用时只需要提供输入,并获取输出就可以了。
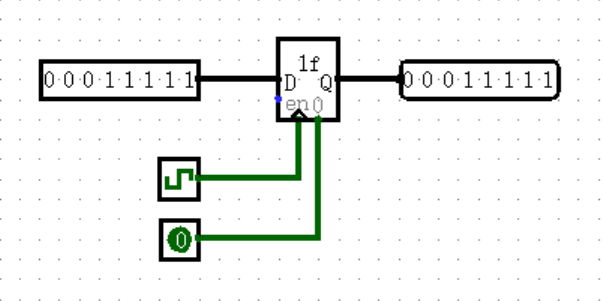
在界面的右上角,有一个绿色的加号,点击它我们就可以创建一个新的模块。双击列表中的新模块,我们就可以切换到新模块的编辑模式。在图中,我们创建了 Gated D Latch 模块,在其中画了一个带使能端的 D 触发器。
在编辑完新模块之后,我们就可以进入左上角的模块外观编辑,编辑并检查当前模块的外观。这里就像一个画图软件一样,你可以用各种奇葩的图形随意更改这个模块的外观,方形、梯形、三角形,甚至圆形,这里可以随心所欲!
此外,输入和输出的位置都是可以移动的,建议把它们之间的距离调大一点,这样在使用的时候布线会更加舒服。在调整之前别忘了左键单击一下它们,在右下角看看它们对应的是不是你想象的那个接口!
如果输入和输出比较多的话,我们还可以使用左上角的工具在模块上添加文字,妈妈再也不用担心我找不到对应的的接口了!
现在,我们双击 main 模块,回到 main 模块中,然后单击 Gated D Latch 模块,就可以使用我们刚才创建的模块了!现在我们可以准备起飞了!
【D触发器】
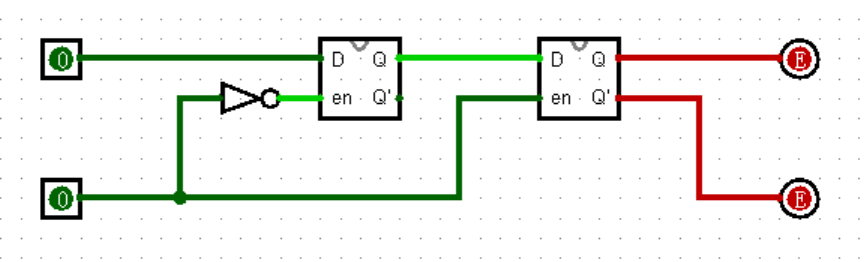
现在,我们搭建这样一个电路:
这就是 D 触发器(D Flip-Flop),由两个 D 锁存器组成,两个使能端的值相反。或许要肉眼看出它的作用还是有点太难了,不过你可以跟着下面的操作去做,在我的引导下逐渐发现它的作用。
现在,让我们保持使能端为 0 ,改变输入 D 的值,观察电路的输出有变化吗?(并没有)
然后,让我们保持使能端为 1 ,改变输入 D 的值,观察电路的输出有变化吗?(还是没有,真让人疑惑)
接下来,按以下步骤进行操作:
- 将输入 D 置为 1 ;
- 将使能端置为 1 ;(输出变为了 1 !)
- 将输入 D 置为 0 ;
- 将使能端置为 0 ;(输出并没有发生变化)
- 将使能端置为 1 ;(输出变为了 0 !)
到这里,你能发现 D 触发器的作用了吗?实际上,当且仅当使能端由 0 变为 1 的一瞬间,输入端 D 的值才会被输出!我们为这个瞬间起一个名字,就叫作“上升沿”;反之,使能端由 1 变为 0 的一瞬间,就叫作“下降沿”。
然而,求知欲超强的你一定会问了,这是为什么呢?且听我细细为你分析:
在上一节我们讲过,当 D 锁存器的使能端关闭时,它便保持当前的输出不变。在这个电路里,我们根据使能端的值进行分析:
当使能端为 0 时,前一个 D 锁存器的使能开启,将输入端的数据输出至两个锁存器之间;然而后一个 D 锁存器处于关闭状态,不能将数据输出至输出端,于是当前的数据就滞留在了两个锁存器之间。
当使能端为 1 时,前一个 D 锁存器的使能关闭,不再接收输入端的数据,而是保持之前的输出(即滞留在两个锁存器之间的输出)不变;此时后一个 D 锁存器的使能开启,将滞留在两个锁存器之间的值输出出来。
需要注意的是,使能端为 1 时输出的并不是当前输入端的值,而是在切换使能时滞留在两个锁存器之间的值,也就是切换使能时的一瞬间输入端的值,这从上升沿之后无论如何改变输入端的值,输出端的值都不再变化可以看出。
在左侧的 Memory 文件夹中,有 Logisim 内置的 D 触发器(D Flip-Flop)模块,你可以用它试一试,看看和我们自己做的是不是一样~
(注:如果你觉得不一样的话,那你一定是把上下搞反了,Logisim 的 D 触发器,上面的三角才是使能端( Logisim 所有的元件标三角的地方都是用来接 Clock 的使能端),下面的 D 才是输入端,现在知道模块外观的重要性了吧(笑))
刚才我们提到了 Clock ,现在你可以试着用 Clock 替换使能端的输入,接在左上角的三角处。现在你可以用 Simulate 中的 Ticks Enabled 来让使能端自动翻转了!
最后,我们来练习写一下 D 触发器的逻辑表达式。我们接下来还会遇到许多触发器,使用他们的逻辑表达式(这里称为特性方程)可以更直观地理解它们的作用。
D 触发器的特性方程是:
$$ Q_{n+1} = D $$
这里的 n+1 是什么意思呢?事实上,这是表示时序的一种记法,n+1 表示的是下一个周期。在其它触发器中,我们会遇到当前周期的输出会重新参与进运算,影响下个周期输出的情况,这时候为了区分两个周期的输出,我们用 n 表示当前周期,而用 n+1 表示下一个周期。
【T触发器】
除了 D 触发器之外,Logisim 中还有三种触发器,这些触发器虽然在实验中不会遇到(其实 D 触发器也不会),但是却是理论考试的常客,所以还是有必要介绍一下。
T 触发器(T Flip-Flop)相信 Minecraft 牢玩家都有所耳闻。在游戏中,使用发射器装细雪桶,再配合红石比较器就可以形成一个简单的 T 触发器,可以把按钮变成拉杆。用我们课程的语言来说,就是在 Clock 的每个上升沿都翻转一次输出,现实中的 T 触发器也正是这样。和 D 触发器不相同的是,当 Clock 处于上升沿的时候,输出端不再输出上升沿时输入端的值,而是当上升沿时输入端为 1 时,翻转输出端的值。所以,你能写出它的特性方程了吗?(答案如下:)
$$ Q_{n+1} = Q_n ^{\space\space\space} T $$
(这里的尖角表示异或)
使用与或非的形式,也可以写成:
$$ Q_{n+1} = T\overline{Q_n} + \overline{T}Q_n $$
(在数字电路的表达式中,用加号代替或,用乘号(或者直接省略)代替与,用上划线代替非,这种写法在电子电路领域比较常见)
【JK触发器、SR触发器】
JK 触发器(J-K Flip-Flop)和 T 触发器很相似,只不过输入端变成了 J 和 K 两个。当 J 和 K 的值相同时,它和 T 触发器别无二致;而当 J 和 K 的值相反时,输出端的值将会被固定为 J 的值。它的特性方程如下:
$$ Q_{n+1} = J\overline{Q_n} + \overline{K}Q_n $$
SR 触发器(S-R Flip-Flop)又和 JK 触发器很相似,在 S 和 R 的值不全为 1 时,它的表现和 JK 触发器完全相同;而当二者的值全为 1 时,它维持原输出不变,和 SR 锁存器一样,这种情况实际上是“非法”的。它的特性方程是这样的:
$$ Q_{n+1} = S + \overline{R}Q_n $$
(其中 S 和 R 不能同时为 1 )
【寄存器】
在从最基本的或非门一步步构建出各种触发器之后,我们终于要实现最开始的目标了,那就是对输出的存储。实际上,我们已经完成了这个工作,D 触发器其实就是一个非常良好的存储元件。它的输出只有在每个上升沿才会改变一次,在这一个周期内,这个值被完整地保存下来了。而且这个被保存下来的值也可以像在其它触发器中一样,用于计算下个周期输出的值,这一点我们将会在接下来状态机的学习中了解到。
唯一美中不足的是,D 触发器只能保存一位的值,这显然不太够用,于是有了寄存器(Register)。它其实就是一个可以支持多位的 D 触发器,用法和 D 触发器基本是相同的。
这里我们有两个需要注意的点:第一个点就是寄存器显示的数字为 16 进制,第二个点就是下方的复位信号。当我们将复位信号置 1 时,寄存器的值立马被清零,这种复位方法被称为异步复位,这里的异步指的是复位与 Clock 上升沿异步,不要记混了哦。
相对地,同步复位指的是只有当 Clock 上升沿的时候才检测复位信号是否置 1 ,如果为 1 ,则在该上升沿将寄存器清零。
至此,我们一步一步构建出了 Logisim 中最基本的存储元件,在下一节中,我们将会介绍由它诞生的壮观世界。
1.6 寄存器后日谈
寄存器可以说是 Logisim 中最基础的存储元件了,就像编程中的变量一样。有了它,我们的电路才能够成为跑起来的“程序”,而不是一个语句,一个算式。作为构建起时序电路的基石,有了它,我们的 Logisim 世界又将发生什么变化呢?
【其它存储元件:RAM 和 ROM】
寄存器就像程序中的变量,它小巧而方便,可以随时取用。然而,如果想存取极其大量的数据(比如从文件中读写),寄存器的位宽可能就不太够用了,于是我们就需要更大的“寄存器”:RAM 和 ROM 。
我们先讲解更简单的 ROM 。ROM 是只读的存储器,也就是说,在程序运行的过程中,我们不可以对这个存储器进行存入的操作,只能对里面的数据进行读取。如果想写 ROM 中的内容,则需要在程序运行前就做好。
首先我们学习如何向 ROM 导入数据。右键 ROM ,选择 Edit Contents ,我们就可以进入 ROM 的编辑页面,看到 ROM 中的全部数据。左键点击其中任意一个数据,我们就可以用 16 进制编写选中的数据。当然,当需要输入数据的量特别大时,我们肯定不能用手一个一个输入进去,这时就需要使用文件进行导入。
使用文件导入也非常简单,只需要使用最简单的 txt 文件即可。首先,我们需要在文件的第一行写上一句魔法咒语:v2.0 raw ,然后用 16 进制依次写下每个数据就可以了!下面展示了上图中数据的源文件其中的一小段内容:(注:这段内容是有意义的哦,相信以后你一定能够读懂!)
1 | v2.0 raw |
(这个省略号不是源文件中的内容,它真的就表示省略下文)
点击编辑页面下方的 Open(不是左上角 File 里的那个!),就可以选择数据文件进行导入。导入完成之后直接退出即可,不需要点编辑页面下方的 Save(那个是将当前 ROM 中的数据导出为 txt 文件)。不知道是不是 bug ,在编辑完 ROM 之后需要将工程保存并重新打开,刚才编辑的内容才能显示出来。
ROM 的使用也非常简单,它的左侧有一个输入,表示的是“地址”,注意这里的“地址”和我们以后将要学到并经常使用的内存地址并不是一个意思,这个“地址”你可以完全理解为“数组下标”,表示的就是 ROM 中的第多少个数据(从 0 开始计数,这很计算机)。而右面输出的就是相应位置对应的数据。
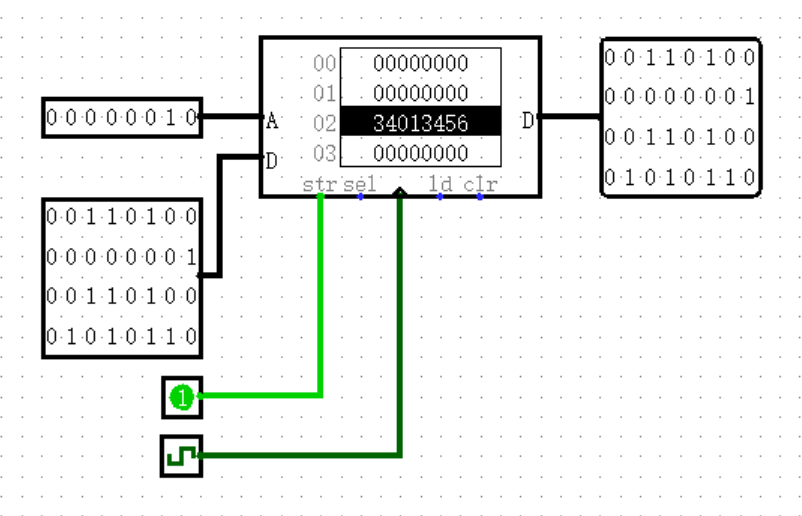
RAM 有关读取的部分和 ROM 是相同的,但它多了写入的部分,也就意味着在程序运行的同时,我们可以修改 RAM 中的值。
在使用之前,我们需要左键 RAM ,将 Data Interface 属性参数手动设置为 Seperate load and store ports ,这是我们课程的统一要求,这样输入的数据和输出的数据就分开了,左侧的 D 处用于向 RAM 输入数据,右侧的 D 处用于从 RAM 输出数据。
相比 ROM ,我们可以发现 RAM 多了三个部分,接下来我将一一讲解:
首先是 Clock ,和寄存器一样,只有当 Clock 处于上升沿时,RAM 才会从输入端读取数据。但是一定要注意,这个 Clock 是不控制输出端的,也就是说只要左侧地址发生变化,右侧的输出会直接发生变化。其实这在寄存器、ROM 那里也都是一样的,回忆一下,如果我们不在 Clock 上升沿就手动改变它们的数据(或者 ROM 的地址),它们的输出是不是也会立刻发生变化?答案是肯定的。
此外就是 str 接口连接的一位信号,它是输入端的使能,也叫作“写使能”,它相当于是数据写入的开关,毕竟我们不需要每一周期都向 RAM 写入数据。只有当它置 1 时,RAM 才会在 Clock 上升沿读取输入端的数据,否则直接“一票否决”写入的权利。
最后就是左侧的 Data 了,没什么好说的,单纯是要写入 RAM 中的数据而已。顺带一提,虽然你肯定已经知道了,左侧输入端向 RAM 输入数据的位置就是左侧“地址”的位置。
另外,向 ROM 导入的数据在关闭文件重新开启的时候是不会清空的,其它所有存储元件(寄存器、RAM 等)中的值都不会被保存在文件中,所以不要手动向寄存器赋初值,否则你会体验到在本地运行时全对,在评测机上全错的快感。
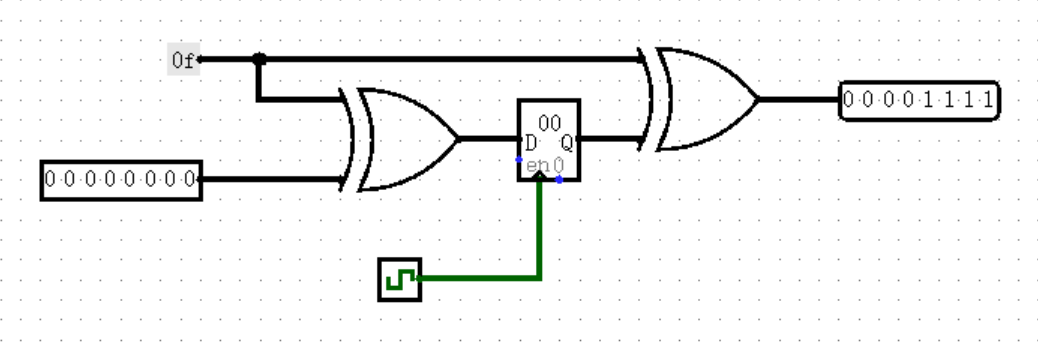
那么,我们要如何在程序开始时向寄存器自动赋初值呢?这时候就需要用到一个非常神奇的结构了:
为什么这个结构能够为寄存器自动赋初始值呢?我们来观察它的构造:
在 Logisim 中,寄存器的默认初始值为 0 ,于是当寄存器中的初始值与我们规定的初始值(图中为 0x0f )异或时,就会输出我们规定的初始值作为结果。
但当我们在输入端输入数据时,寄存器会将我们输入的数据与初始值异或的结果存入其中;同时在另一侧输出时,寄存器中的结果会再次与初始值异或。我们都知道,一个数字异或另一个数字两次,相当于没有异或,也就是 (A ^ B ^ B) == A 。所以,异或了初始值两次的输入值从输出端被输出,相当于没有变化。真的是非常巧妙的结构!
不过这个结构还是有点小缺点的,就是寄存器中的值不再等于我们真正要存储的值了,而是这个值和初始值异或一次的结果,所以我们要特别注意一下,在调试的时候不要以为自己写出 bug 了(笑)!
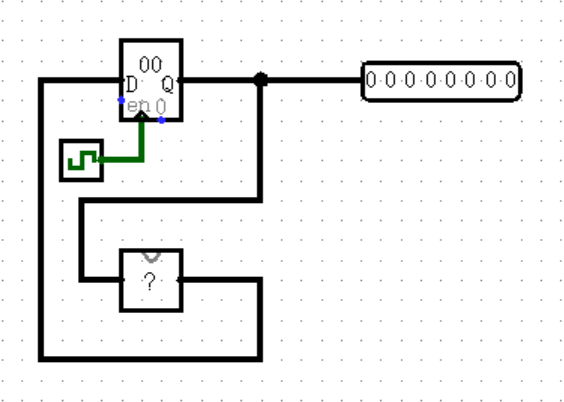
【状态机】
发明状态机的人绝对是个人才,如同左脚踩右脚上天,一个简单的结构就可能演化出无限可能。
在我看来,状态机最特别之处就是它的输出经过一些运算,会反过来成为下一个周期输入的一部分,这样就能够无限地递推下去。
下面是一个最简单的状态机,它甚至不需要输入,只需要自给自足就可以有无限的输出:
(这个图画得比较丑陋,是因为 ? 处的输入在左边,输出在右边,这样更方便理解。你当然可以在自定义模块外观时把它们反过来,那样就会很好看)
当然,你肯定会问 ? 处模块的内容是什么,事实上,这个模块可以是任何内容,正是这个模块赋予了状态机无限的可能。
比如,你想让寄存器中的数字每个周期都增加 1 ,那么你只需要在 ? 处编写一个逻辑,实现 output = input + 1 即可。
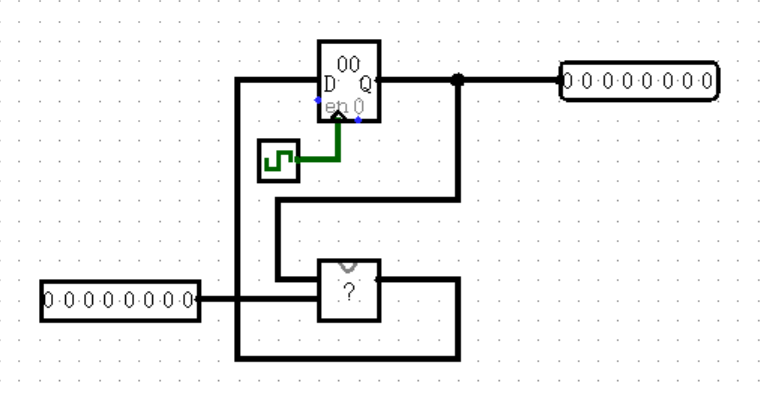
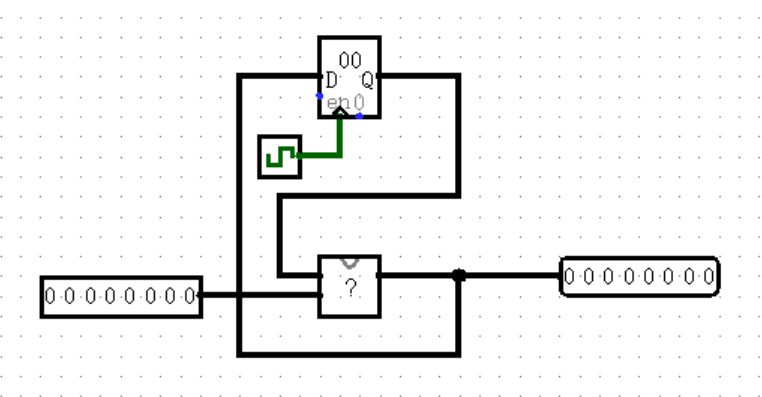
这只是最简单的状态机,可以说是状态机的冰山一角了。比如,我们更常见的是有输入的状态机,它与当前周期的输出一同进行运算,得出下一个周期的输入:
上面给出了两种有输入的状态机,它们之间有什么区别?输出的位置是不同的,上面一幅的输出紧跟寄存器,位于 ?(称之为“状态转移”)之前;下面一幅的输出则位于状态转移之后。前者被称为 Moore 型状态机,后者则被称为 Mealy 型状态机。
我最开始学习状态机的时候,完全分不清这两者有什么区别,一是因为指导书的定义太过正式(并不是本书的定义方法,甚至图也不太一样),二是因为真正做题的时候碰到的状态机都奇形怪状,长得一点也不像上面的“标准”状态机。
后来我才发现,其实它们的区别真的非常非常明显。Moore 型状态机的输出在状态转移之前,所以无论输入端是什么,运算后的结果都只能在下个周期 Clock 的上升沿写入寄存器之后才能被输出了,这就是指导书中说的“ Moore 型状态机输出与输入无关”;而 Mealy 型状态机的输出在状态转移之后,所以它的输出会实时更新当前输入参加运算后的结果,而不需要等到下个周期才能给出了,这就是指导书中说的“ Mealy 型状态机输出与输入有关”。
读懂这段话,你也就能明白所谓的“ Mealy 型状态机比 Moore 型状态机早一个周期”是什么意思了。实际上这句话并不严谨,只有当且仅当 Clock 上升沿时改变输入端的数据才是如此,更正常的说法是:输入端输入本周期的数据,Mealy 型状态机的输出端立刻出结果,Moore 型状态机的输出端要到下一个 Clock 上升沿才出结果。
关于状态机的内容,我们暂时先讲到这里。虽然目前为止我们了解得看似不多,但已经足够衍生出巨量的可能了,快去结合实际问题试试吧,你会看到更多奇形怪状的状态机的!(笑)
1.7 本章结语:再见,Logisim!
经过一段漫长的学习,我们对 Logisim 的学习也要告一段落了!能坚持看到这里的你也非常不容易!在这漫长的一章中,我们学习了 Logisim 这款软件,了解了数字电路的基本知识,认识了许多数字电路元件,更是接触到了时序电路、状态机这些复杂高深的知识。虽然我们即将暂时告别 Logisim ,但在 CPU 搭建时,我们会再见的!希望那时的你已经学到了更多计组知识,并将它们与这一章的内容融会贯通,产生更深刻的了解,将 CPU 轻松拿下!
第二章:汇编语言 MIPS
2.1 汇编语言与 MIPS 简介
或许你在过去的学习中已经听说过了汇编语言,在这里,我们还是对它进行一个正式的介绍吧。在学习 C 语言的时候,我们也许会有这样一个问题:对于一台计算机来说,它只能理解 0 和 1 ,那么它是如何能够理解并执行我们编写出来的代码的呢?或者说,我们的代码是如何被一步步转化成 0 和 1 的呢?其中最关键的一步就是将代码“编译”为我们接下来要学习的“汇编语言”。
汇编语言也是一种编程语言,但是相比 C 语言来说,它是一种更“低级”的编程语言。这也就意味着,它能够实现的操作种类更少,相比更高级的语言代码量往往更大,但也更加接近计算机的底层架构。
接下来,我们就来认识一下我们将要学习的汇编语言 —— MIPS 。作为一门古老的汇编语言,MIPS 能够实现运算、对内存进行访存、跳转、条件赋值、条件跳转等多种操作,同时固定 32 位的指令也可以让我们在后续设计 CPU 时能够更加方便。是我喜欢的语言,直接开学!
2.2 MARS 简介
工欲善其事,必先利其器。类比 C 语言,它只是一种编程语言,要想让它能够跑起来,还需要一款合适的 IDE ,比如大家最喜欢的 devcpp 和 vscode 等等。所以,MIPS 语言也需要一款能够真正让它跑起来的 IDE ,那就是 MARS 。课程组已经亲切地为我们提供了这款软件,我们下载后打开即可。在之后,为了方便大家完成后续的实验任务,还会有各路巨佬的魔改版将会流出,大家可以多多关注群聊~
【创建、打开MIPS文件】
在一众软件中,MARS 的界面可以说是最简洁的了。我们进入后,点击左上角的 File ,使用 New 来创建一个新文件,使用 Open 来打开一个新文件,结束编辑后,使用 Save 或者 Save as 保存即可。
【MARS设置】
在正式开始学习之前,我们需要在左上角的 Settings 一栏更改一些设置,将其调整至符合我们课程要求的形状:
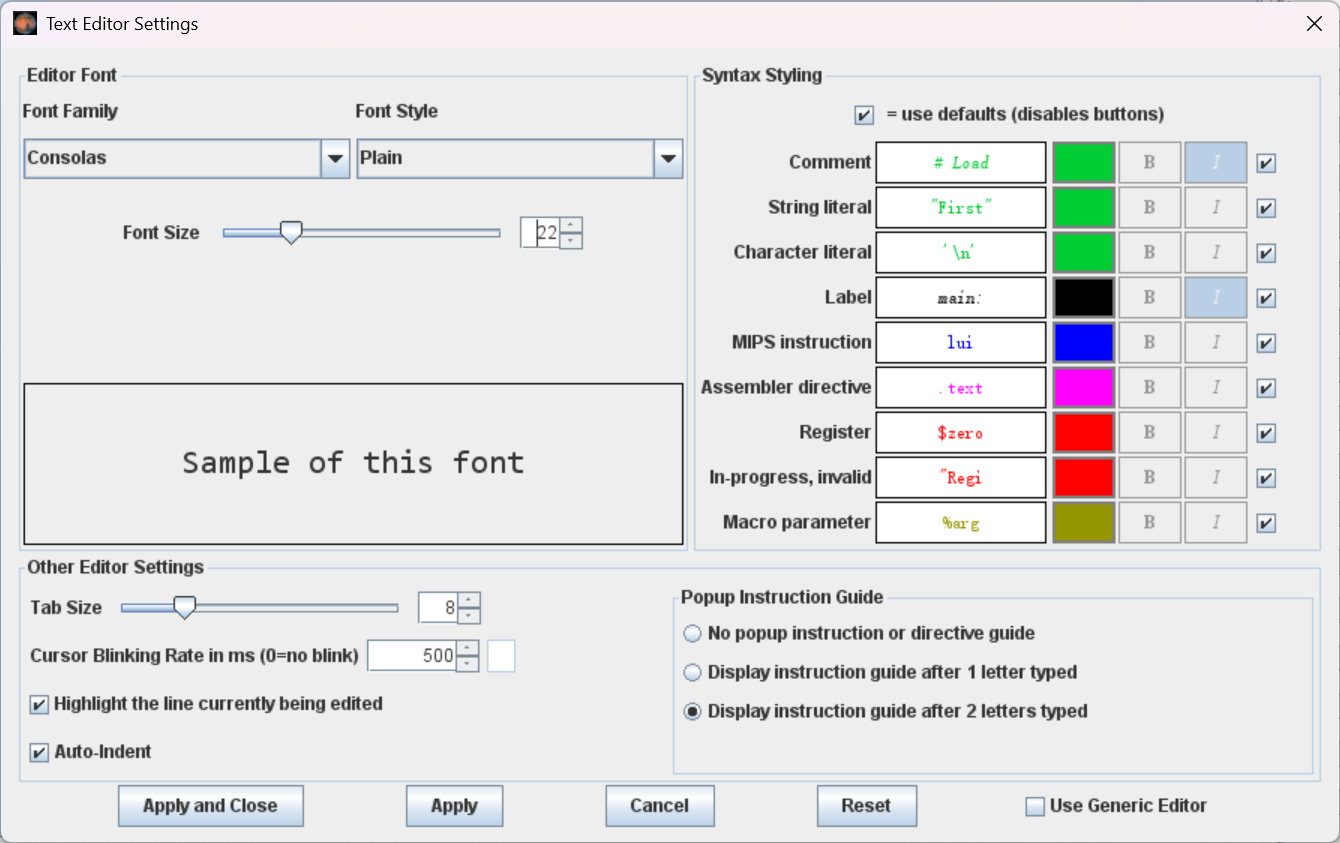
首先点击 Editor ,在 Font Family 处调整字体,在 Font Size 处调整文字大小。我个人喜欢用 22 号的 Consolas 字体,这里可以按照个人喜好设置,其它的设置保持默认即可。
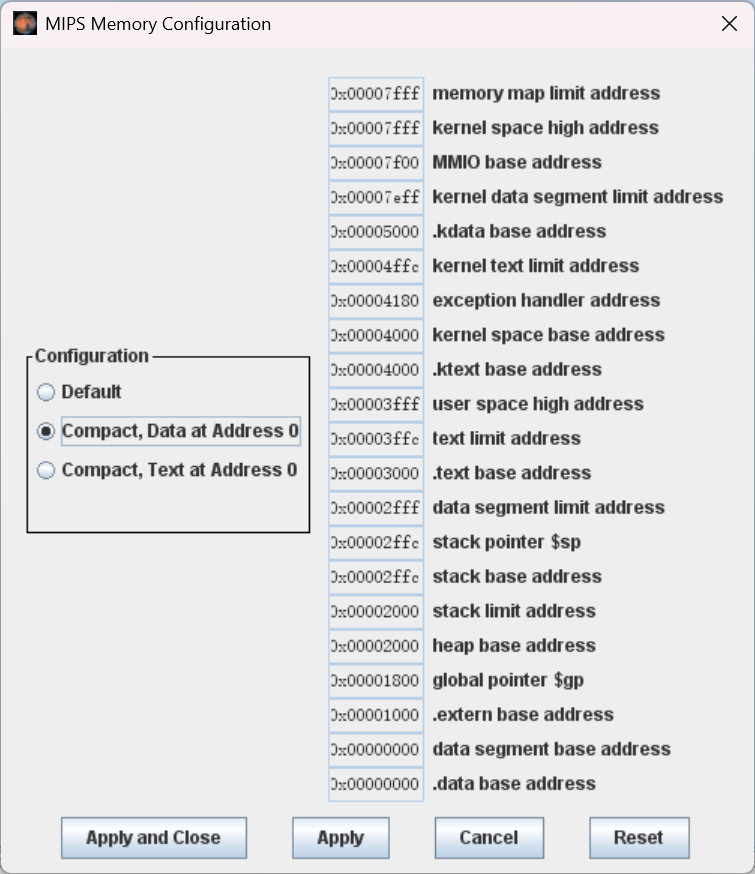
接下来点击 Memory Configuration ,将 Configuration 设置为 Compact, Data at Address 0 。这一步至关重要,如果上机考试忘记调这个,那就等着对着怎么也跑不对的代码干瞪眼吧!(笑)
在 Settings 一栏中还有一个选项是 Delayed branching ,即”延迟槽”,目前我们还不需要知道延迟槽是什么,请务必将其保持关闭,等到我们正式开始写 CPU 了之后才需要开启它。
【调试、运行MIPS代码】
下面我们来学习一下如何调试、运行我们的汇编代码,以附件中的 2.3-1.asm 文件举例。
首先就是按照我们之前的教程,使用 File - Open 打开这个文件,接下来,点击上方工具栏中“扳手和螺丝刀”的图标,进入 Execute 界面:
使用最上方工具栏中的几个运行按键,就可以非常轻松地完成对代码的调试和运行,最左侧还提供了打断点的位置供我们使用。
代码界面除了我们自己写的代码和设置断点的区域外,还有很多信息供我们使用:Address 即每条指令的地址,Code 即每条指令的机器码,Basic 即每条指令和伪指令的翻译。现在我们可能一些不懂,但在之后都会系统地学到,并且要经常使用它们。
寄存器界面和内存界面极大地方便了我们的调试。和 C 语言调试时 IDE 能够实时显示每个变量的值一样,这两个界面也是用来实时显示在寄存器和内存中存储的值的。有关寄存器和内存,我们之后还会再学到。
最后是交互界面,如果我们的代码涉及到输入和输出,就需要在这个界面的 Run I/O 界面下完成,在讲到输入输出的时候我们就会用到它(那可能已经是很后面很后面的事了)。
2.3 MIPS 语法初步
接下来,我们就要正式开始我们的 MIPS 学习了。作为一门编程语言,我们首先要学习的肯定就是它的语法:
【MIPS中的寄存器】
在 C 语言中,我们使用自定义的变量来存储值。然而在 MIPS 中,我们不能自己定义变量,而是只能使用规定的寄存器来进行存储。常用的寄存器有 32 个,名字为 $0 到 $31 ,这 32 个寄存器构成了寄存器堆 GRF 。另外还有一些特殊的寄存器 PC HI LO 等,它们的存取方式和普通寄存器有所不同,我们稍后再介绍。
上述的所有寄存器,每个寄存器都可以存储一个 32 位的值,大小和 int 类型的值相同。
刚才我们提到了 $0 到 $31 这些普通的寄存器,它们是相同的吗?我们可以对它们随意赋值吗?其实并非如此。每个寄存器都有着自己的职能,发挥着不同的作用。
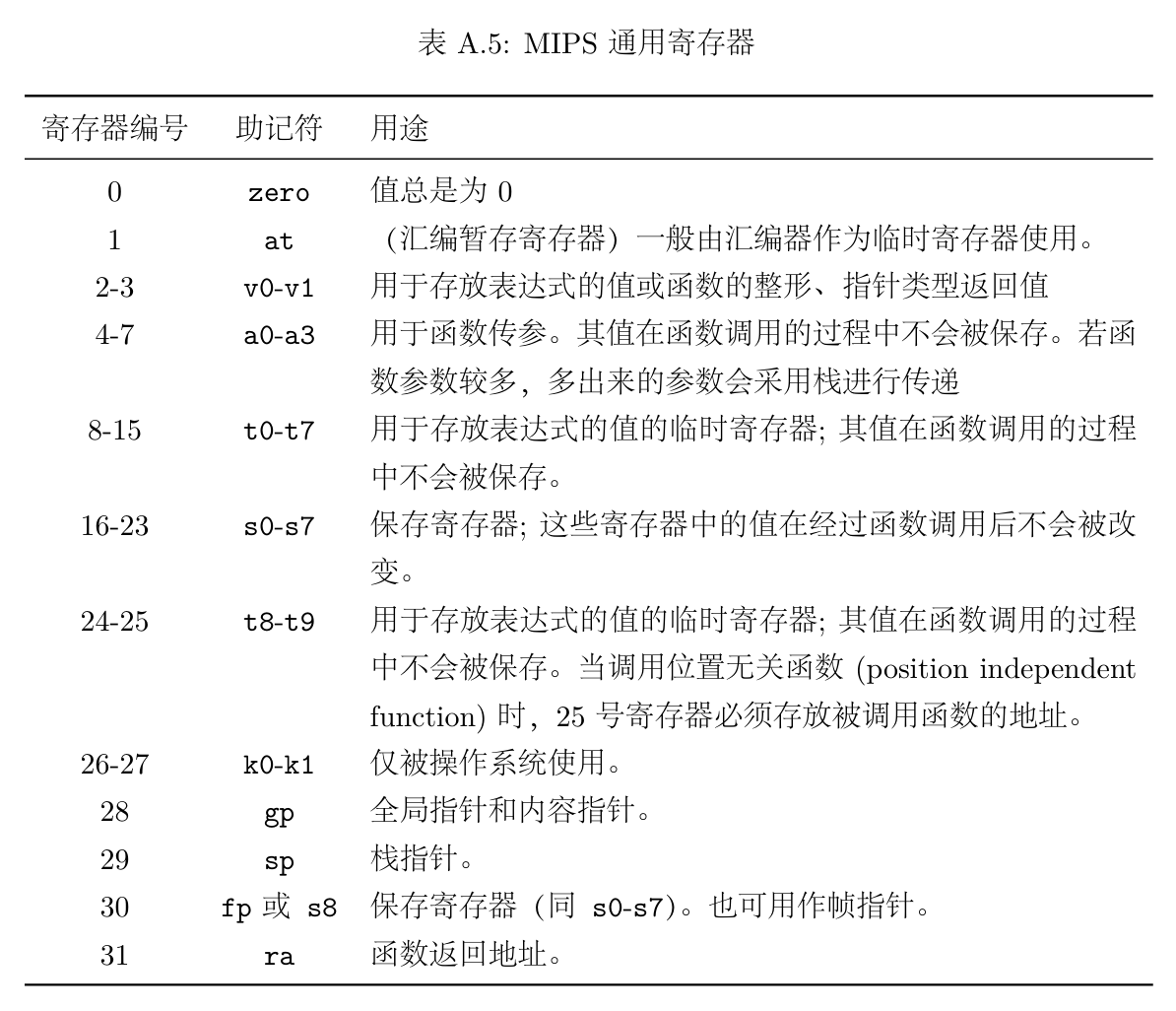
根据它们的作用,我们还为它们起了另外的代号。我们在编写汇编代码时,既可以用它们的“本名”(如 $16 ),也可以用它们的“代号”(如 $s0 )使用它们,二者是完全等价的。
(从操作系统指导书里面抠下来的表格)
我们不需要去背诵每个寄存器“本名”和“代号”之间的对应关系,不过还是要清楚这些寄存器的职能。有些寄存器的性质比较特殊,是不能和其它寄存器混用的,在这里列举几点要点,希望能够帮你规避一些以后可能会出现的奇妙 bug :
$0寄存器不能被赋值,无论如何被赋值,它的值永远为 0 ;$1寄存器会被用在伪指令的展开中(伪指令的概念我们稍后会介绍到),尽量不要使用这个寄存器;$26到$31这几个寄存器都有自己的特殊用途,同样不要使用;$v0和$a0两个寄存器会用于syscall指令的传递参数中,建议不要随意“借用”这两个寄存器,让它们各司其职就好。
那么,说了这么多不能用的寄存器,到底有哪些寄存器是可以放心用的呢?实际上,我们平常会用来作为变量的寄存器一般就只有 $s0 到 $s7 ,和 $t0 到 $t7 两个系列。虽然表格中告诉我们前者一般用于存储定值,后者一般用于存储变量,但其实只是君子协定,即使不遵守也没有问题,只不过美观性上可能会有影响。比如在 t 系列的寄存器全部用光光的时候,我们就可以去 s 系列去“借”一些来用(读书人的事)。其实把 a 系列也加进来,它们三个系列互相借来借去也没什么问题,除了上面提过的 $a0 寄存器不太好惹以外,a 系列的其它寄存器也可以随便拿来用。
(免责声明:我不太建议随便借来借去的这种行为,本来寄存器就没法像变量那样命名,一多起来真的找不到谁是谁,一会儿就乱了)
【MIPS指令:位运算】 and or xor nor andi ori xori
学习了寄存器之后,我们来学习如何使用寄存器进行运算。或许你以为我要从四则运算开始讲起,不过对于计算机来说,四则运算还是有点太难了(笑)还是先从位运算开始讲起吧:
首先是与运算、或运算和异或运算。如果我们想表示 $t2 = $t0 & $t1 ,该怎么编写汇编代码呢?答案是 and $t2, $t0, $t1 。and 表示我们当前使用的指令,后面紧跟着由英文逗号隔开的三个寄存器的名称,需要格外注意的是,运算的结果是写在最前面的,而不是写在最后面。
同样的,如果想表示 $t2 = $t0 | $t1 ,可以使用 or $t2, $t0, $t1 ;如果想表示 $t2 = $t0 ^ $t1 ,可以使用 xor $t2, $t0, $t1 。
如果我们想将其中一个寄存器换为某个定值(在以后我们称这个定值为“立即数”),例如 $t2 = $t0 & 15 ,可以使用 andi $t2, $t0, 15 ,这里的 15 也可以写成 0xf ,即十六进制的表示法也是可以的。同理,ori 和 xori 指令也是相同的用法。
这里需要注意的是,andi ori xori 这一类使用立即数的指令,立即数必须写在第三个寄存器的位置,不可以和前面的寄存器调换!
接下来就是取反运算了,MIPS 指令集中并没有直接给出取反运算的指令,但是我们可以略施小计将其解决。MIPS 指令集中提供了或非运算指令 nor ,我们使用 nor $t0, $t0, $0 即可将 $t0 寄存器的内容原地取反(还记得 $0 寄存器的值永远为 0 这码事吗)。
MIPS 指令集提供给我们的指令十分有限,大家千万不要脑补出一些不存在的指令来!(比如 nori 指令就不存在,再比如两个立即数直接运算的指令也不存在,你可以将立即数赋值到寄存器中再进行计算)如果不确定指令存在与否的话,还是要先查一查指令集来判断!
【伪指令】 move li la
但是凡事也都不是绝对的,虽然指令集里没有这些指令,但是设计者已经料到了你肯定会这么脑补(笑),所以他们允许你这么写,然后将你写出来的“伪指令”转换成一条或者几条合法的指令,从而实现同样的功能。
在使用汇编语言编程时,我们完全可以使用这些伪指令,甚至说我们完全离不开伪指令。我们只需要记住,在之后设计 CPU 时,我们不需要考虑它们就好了。
现在我们尝试在 MARS 中输入下面的代码:
1 | ori $t1, $0, 0xf |
保存后,点击上方“扳手和螺丝刀”的图标,即可进入 Execute 界面。在左上方,我们能够看到刚才的代码被“翻译”成了什么:
可以看到,第一条指令 ori $t1, $0, 0xf 没有发生变化,然而第二条指令 ori $t1, $0, 0xfffff 却被翻译为了 3 条指令。这是因为 ori 指令中的立即数最多只能为 16 位,所以 20 位的立即数 0xfffff 其实是不合法的。不过 MARS 已经帮我们处理好了,就不需要我们考虑太多了。(不过如果期末理论考试考到,可还是要能判断出来它是不合法的哟~)
第三条和第四条指令,明显是缺了一个寄存器,这实际上也是不合法的,然而 MARS 将其解读成了 $t1 寄存器自己或上一个立即数,再赋给自己的过程,相当于是 $t1 |= 0xf 。
接下来我们来输入下面这段代码:
1 | li $t2, 5 |
同样,我们进到 Execute 界面,观察这些指令的“真身”:
可以发现,它们也不是指令集中的指令,而是伪指令。然而,这些指令的作用却非同寻常。li(load immediate)伪指令用于将立即数直接赋值给寄存器,move 指令用于将后一个寄存器的值赋值给前一个寄存器(这里和物理意义上的 move 不相同,原寄存器的值不会被清零,更像是 copy )。
la(load address)指令理解起来有些复杂,也没那么常用,不过我记得我还是用过一次,所以还是简单了解一下。在 MIPS 汇编代码中,我们可以使用自定义的标签名 + 冒号为一个位置打上标签(如上述代码中的 label1: ),标签本身不是汇编指令,只不过是一种便捷的写法而已。在 Execute 中我们能够清楚地看到原来标签的位置被替换为了它的地址 0x00003008(至于为什么是这个地址,我们过后再研究)。la 和 li 的作用比较相似,后者将立即数存入寄存器内,前者则是将地址存入寄存器内。
【MIPS指令:四则运算之加减法】 add sub addu subu addi addiu
接下来,我们来了解一下四则运算。四则运算和位运算最大的不同,就是四则运算会面临着两个棘手的问题:正负性和位溢出。
首先来谈正负性的问题,其实这根本就不是个问题。如果你是补码领域大神的话,你就会发现,在不考虑位溢出的情况下(这里“不考虑位溢出”的意思是发生溢出时会将溢出位舍去,相反“考虑溢出”的意思是如果发生溢出直接报错),二进制补码的正负性其实是相同的,这也正是补码的优越之处。不信可以看看下面这些例子:
在 32 位的条件下,0x3 + 0xffffffff 的结果是多少?你的做法或许是这样的:首先,你发现 0xffffffff 的最高位是 1 ,于是断定它是负数,将其一段操作转换成 -1 ,再与 0x3 相加,得到结果 0x2 。但实际上,我直接把它们两个相加,结果就是 0x100000002 ,舍去溢出的最高位,直接就得到了 0x2 。
再举一个例子,同样是在 32 位的条件下,0xfffffffd - 0xffffffff 的结果是多少?细心的你可能会将这个式子转换成 (-3) - (-1) ,结果是 -2 ,也就是 0xfffffffe 。但是我不管正负,直接进行运算,发现被减数小于减数,我直接在被减数前面补一个溢出位 1 ,于是原式变成 0x1fffffffd - 0xffffffff ,结果等于 0xfffffffe 。
于是我们可以看出,在不考虑位溢出的情况下,我们不需要先确定一个补码的正负性,再根据其正负性进行运算,而是直接按照加减法规律对其进行运算即可。addu 和 subu 就是这样的指令,它们在进行加减法时,完全不需要考虑溢出位的问题,出现溢出直接舍去最高位,就是这么简单粗暴。
相反,add 和 sub 两条指令就要心思缜密一些,它们在发生溢出时不会计算,而是会发生报错,抛出异常。这样我们刚才“无论正负直接计算”的理论就要站不住脚了。例如上面的两个例子,直接计算时都出现了位溢出的现象,但如果考虑它们的正负性,你就会发现,一个是 3 + (-1) ,一个是 (-3) - (-1) ,都是十以内加减法(当然,是正负十,笑),无论如何也谈不上溢出嘛!这就要提到了,上述的算法固然能保证结果正确,但它的计算过程却是天马行空的,所以在这个过程中就会出现“本来没溢出却溢出了”的情况。所以在判断是否溢出时,还是需要按照老方法规规矩矩来做。
上述四条指令的用法都是 xxx $t2, $t0, $t1 ,依旧是被赋值的寄存器打头,进行运算的两个寄存器殿后。(有 3 个寄存器的指令都是这样的,以后就不单独再提了)
此外,add 和 addu 两个指令还有它们的 i 版本addi 和 addiu(subi 和 subiu 是伪指令),同样,它们的用法就是 xxx $t2, $t0, imm16(imm16 代表 16 位的立即数,超出 16 位的话是伪指令)。
【MIPS指令:四则运算之乘除法】 mult div mfhi mflo mthi mtlo
刚才我们讨论了加减法,到了乘除法这里就不只是溢出一位这么简单的问题了。众所周知,两个 32 位的数字相乘,最多能达到 64 位,如果说结果超出 32 位的乘法都算溢出,舍掉或者报错好像都不太合适。这时候天才的你就想到了,将结果分为高 32 位和低 32 位,分别存入两个寄存器中不就好了嘛!恭喜你,你发明了 HI 寄存器和 LO 寄存器!
在乘法运算中,我们只需指定两个乘数所在的寄存器即可,格式为 mult $t0, $t1 ,运算的结果中,高 32 位自动存储在 HI 寄存器中,低 32 位则自动存储在 LO 寄存器中。
这两个寄存器是特殊寄存器,它们不能直接参与到运算中,如果想使用其中的数据,需要先使用指令将它们取出来,这就需要用到 mfhi 和 mflo 指令了。使用 mfxx $t0 ,就可以将 HI 或 LO 寄存器中的值取出到 $t0 寄存器中。当然,还有反过来的指令 mthi 和 mtlo ,使用 mtxx $t0 就可以将 $t0 寄存器的值写入 HI 或 LO 寄存器。
另外,mult 指令也是有符号的运算,所以 0xffffffff * 0xffffffff 的结果不是 HI = 0xfffffffe LO = 0x00000001 ,而是 HI = 0x00000000 LO = 0x00000001 。相当于 (-1) * (-1) = 1 而已。你可能会问为什么加减法可以无所谓有无符号,计算出来的结果是相同的,而乘法却不可以。我会说其实二者是一致的,你之所以会认为计算的结果是相同的,是因为我们把溢出位舍掉了。在讲加法的第一个例子中,我们在计算 0x3 + 0xffffffff 时,得到的结果实际上是 0x100000002 ,我们将 32 位的溢出位舍掉之后得到了结果 0x2 ,乘法也是同理。如果仅保留低 32 位,也就是 LO 的部分,我们会发现上面两个式子的 LO 是一致的,这也就印证了我之前的说法。而 HI 作为“溢出”的 32 位,两种算法结果不同也是正常的。
接下来就是除法了,它的格式为 div $t0, $t1 。我们知道除法当然不涉及到位溢出的问题,但是却有商和余数两个结果,所以我们就可以将 HI 和 LO 两个寄存器充分利用起来,规定用 LO 寄存器存储商,HI 寄存器存储余数。这里还是需要注意一下,非常容易记反的。
有同学可能会问,在 MIPS 中,当除数或被除数为负数时,余数的正负性该如何判断。直接说结论,和 C 语言中的规定相同,被除数为正数时,余数为 0 或正数;被除数为负数时,余数为 0 或负数。看下面这个表格就明白了:
| 被除数 | 除数 | 商 | 余数 |
|---|---|---|---|
| 7 | 3 | 2 | 1 |
| 7 | -3 | -2 | 1 |
| -7 | 3 | -2 | -1 |
| -7 | -3 | 2 | -1 |
【位、字节、半字、字】
我们马上就要进入内存的学习了,在接下来的部分,我会大量地使用标题中的这些概念。如果你对这些概念还不是特别清楚,请务必好好看看下面的讲解,打下一个坚实的基础:
在之前的内容中,我们往往都使用“位”(bit)这个单位来形容一个二进制数,很简单,1 “位”就代表着一个二进制值,它可能是 0 ,也可能是 1 。二进制数 0b10101 就是 5 位,十六进制数 0xabc 中的每个数字都可以转换为 4 位二进制数(例如 0xa 等于 0b1010 ),所以它有 12 位。
另外一个很常用的单位是“字节”(Byte),1 字节等于 8 位,即 1 Byte = 8 bits 。对于一个 32 位的寄存器,它的大小就相当于 4 字节。字节是地址的基本单位,我们马上就会讲到。
如果再大一点的话,2 字节(16 位)等于 1 “半字”(halfword),4 字节(32 位)等于 1 “字”(word)。于是一个 32 位的寄存器就是 2 半字或 1 字。
【地址】
在上一节,我们学习了如何使用 32 位的寄存器来存储数据,以及如何使用指令对寄存器进行运算、赋值。然而,对于一个庞大的程序来说,所有的数据肯定不可能全部存储在寄存器中(那我开个 int [32] 的数组你不直接炸了吗),所以我们开辟了一个庞大的、连续的内存空间,用来存储更多的数据。
(当然,在内存空间外还有更大的外存空间,这一部分就是理论课的内容了,在这里我们不过多提及)
以防你忘了 MARS 的内存界面长什么样,在这里再贴一张:
刚才我们提到,这一片内存空间是非常巨大的,所以我们并不会像寄存器那样,给每个 32 位的空间都起一个名字。但正因为它是连续的,所以我们可以像数组下标一样,从 0 开始为每块空间编号,这就是内存空间的地址。
这里要注意,每个地址代表的空间不是 1 位,也不是 32 位,而是 8 位(1 字节),这也就是在说,字节是地址的基本单位。
举个例子来说,一个 32 位的寄存器中存储着数据 0x12345678 ,我将其写入地址为 0x0 的位置,此时从 0x0 开始第一个没有写入数据的地址是哪个?答案是 0x4 。因为 0x12345678 有 32 位(4 字节),占据了 0x0 0x1 0x2 0x3 这 4 个地址的空间,所以答案是 0x4 。
接下来我们来研究一个更有意思的问题,0x0 0x1 0x2 0x3 这 4 个地址对应的数据分别是什么?先别急着回答,好好想一想。
答案是 0x78 0x56 0x34 0x12 !你答对了吗?或许你会感到很诧异,因为这个答案可能和你想象中的正好相反。但请一定记住,一个数字的最右侧才是最低位,如果按照从低位到高位的顺序依次取 8 位出来,最先取到的 8 位一定是 0x78 ,对应的地址是 0x0 ;紧接着才是 0x56 ,对应 0x1 ;然后是 0x34 ,对应 0x2 ;最后是最高 8 位的 0x12 ,对应 0x3 。
关于地址的知识点很难,但是也极其重要。如果上面讲的知识点没有大彻大悟的话,就会对后面的内存访存指令的理解产生困惑,然后对 CPU 搭建时地址的变换产生困惑,然后对期末理论考试的许多计算题产生困惑,然后对操作系统课程的内存管理产生困惑,最后就变成系统能力废人了。作为这本书的作者,我可能真得让你清楚清楚,真的。
【MIPS指令:内存访存之按字访存】 sw lw
有了上面的知识做铺垫,我们就可以来讲解一下对内存进行读取和存储的指令了。
首先我们来研究一下最常用的两个指令 sw 和 lw ,全称 store word 和 load word 。顾名思义,它们的作用分别是向内存中一次性写入或读取一个字。
这两条指令的用法是我们以前没有见过的。sw 指令使用 sw $t1, imm16($t0) 或 sw $t1, label($t0) 两种方法来调用,表示将 $t1 寄存器中的内容写入“ $t0 寄存器中存储的值 + imm16 立即数 或 label 标签表示的地址”这个地址中。
说起来有些复杂,我们举几个例子来理解一下:如果 $t1 = 0x12345678 $t2 = 0x00000007 ,我想使用这两个寄存器将 $t1 中的内容分别存储至 0x8 和 0x4 的内存地址中,该如何编写指令呢?答案是 sw $t1, 1($t2) 和 sw $t1, -3($t2) 。是的,这里的立即数可以是负数。这就是使用寄存器 + 立即数构造地址的方法。
再举一个例子,假如我想利用一块连续的内存空间实现一个 int 类型的数组 arr[] ,如果 arr[0] 的地址为标签 arr ,那么我该如何将 $t1 寄存器的内容存储至 arr[3] 呢?
首先我们需要知道,int 类型变量的大小是 32 位,所以数组中的每个数字都应该占据 4 个地址,于是我们能够得到这样的结论:如果 arr[0] 的地址是 x ,那么 arr[3] 的地址就应该是 x + 12 。
这时候,很多初学者就会犯迷糊了,直接把指令写成了 sw $t1, 12(arr) 。NO!!!!!这里是非常容易犯的错误。我们的惯性思维告诉我们,括号里面的是一个基地址 base ,括号前面的立即数是在基地址上的小范围偏移 offset ,所以自然而然地就写成了上面那样。
然而,我们一定要回归到定义,在之前学习 la 指令的时候我们能够发现,在执行 la $t0, label 指令的时候,label 会被自动替换为一个立即数,而不是某个寄存器。所以在指令 sw $t1, label($t0) 中,标签 label 替换的实际上是立即数 imm16 的位置,而不是括号中的寄存器。
这道题正确的解答方法是,先将 12 存储到某个寄存器中,如使用 li $t0, 12 ,再执行 sw $t1, arr($t0) 。这就有点像 C 语言中 arr[3] 等价于 3[arr] 一样,非常有趣的小知识,一定要记牢!
学会了 sw 指令,lw 指令也就可以直接出师了。它们两个的用法完全相同,只不过 lw 指令是把后面地址中的内容写入前面的寄存器中罢了。
关于 sw 和 lw 还有一个要点,当计算出要访问的地址后,若地址不存在或非法(比如地址为负),则会直接发生错误,抛出异常。另外,计算出来的地址必须是 4 的倍数,否则同样会发生错误,抛出异常!
下面是一个小测验时间,本关考验你的内存访存功夫,请听题:在之后的学习中,我们会经常用到这条指令 lw $t0, 0($sp) ,既然偏移值是 0 ,那么它和这条指令 move $t0, $sp 是不是等价的呢?
答案是:两条指令并不等价。因为前一条指令中,$sp 寄存器中的数据代表的是一个地址,我们需要根据这个地址到内存中找到相应的数据,将内存中找到的这个数据赋值给 $t0 ;而后一条指令是直接将 $sp 寄存器中的数据赋给了 $t0 。二者是截然不同的!
另外一个小测验,请听题:和上一道问题很相似,指令 lw $t0, label($0) 和 la $t0, label 又是否是等价的呢?
答案是:两条指令依旧不等价。在前一条指令中,我们根据 label 标签表示的地址在内存中找到相应的数据,将内存中找到的这个数据赋值给 $t0 ;而在后一条指令中,我们直接将 label 标签表示的地址赋给了 $t0 。
不知道你是否答对了这两道问题。想当年这两个疑问也曾难倒过我,如果你能不假思索地理清这几条指令之间的关系,那么你的内存访存功夫就已经十分到家了!如果你全部都答错了,那就还是结合附件中的代码,好好领悟一下这一部分的精髓吧!
【MIPS指令:内存访存之按半字、字节访存】 sh lh sb lb
学习完了按字访存,我们来研究一下更灵活的按半字、字节访存。
sh lh 指令,全称为 store halfword 和 load halfword ,用于将一个半字(2 字节,16 位)的数据从寄存器写入内存,或从内存读取到寄存器。
sb lb 指令(并非很优雅的名字),全称为 store byte 和 load byte ,用于将一个字节(8 位)的数据从寄存器写入内存,或从内存读取到寄存器。
这四条指令的用法都和 sw lw 一模一样,在此就不多赘述了,但还有一些小细节是需要我们注意的:
第一就是六条指令对地址的要求并不相同。经过计算得到的地址,除不能是非法地址外,sw lw 指令要求必须是 4 的倍数,sh lh 指令则要求必须是 2 的倍数,而 sb lb 指令没有倍数要求。
第二就是访存前后寄存器内数据的变化。在学习 sw 和 lw 时,我们并没有考虑太多,执行指令时只需要把 32 位的数据整个从寄存器中搬到内存中,或者把 32 位的数据整个放到寄存器中就可以了。然而,当执行后四条指令时,我们要访存的数据不足 32 位,对寄存器中的数据,我们应该如何操作呢?
首先是 sh 和 sb 指令,比如当执行指令 sb $t1, imm16($t0) 时,$t1 寄存器内的数据是 0x12345678 ,超过了 8 位,该如何是好呢?答案是抛弃高出来的位数,只向内存的相应位置写入最低 8 位即可,即 0x78 。
其次是 lh 和 lb 指令,比如当执行指令 lb $t1, imm16($t0) 前,$t1 寄存器已有数据 0x12345678 ,将要被从内存读取到寄存器中的字节是 0x00abcdef 中的 0xcd 字节,那么读取到寄存器中的结果如何呢?答案是 0xffffffcd 。读取到的字节会被存储在寄存器中的最低位,然后符号扩展至 32 位。
【MIPS指令:绝对跳转指令】 j jal jr jalr
MIPS 语法中的跳转指令虽然不多,但作用可谓是非常之大。像 C 语言中的 if 条件分支、while 循环和 for 循环,在 MIPS 中都需要用到跳转指令才能实现。下面我们来学习 MIPS 中的 4 条绝对跳转指令 j jal jr 和 jalr 。
跳转指令其实就类似于 C 语言中的上古禁术 goto ,不知道大家有没有斗胆用过(我是真用过,笑),这下属于是不得不用,可以用个爽了。
j 指令的用法只有一种,就是 j label 。只要把 label 标签写在要跳转的指令前一行,就可以在运行完 j 指令后跳转到该指令。例如下面的例子:
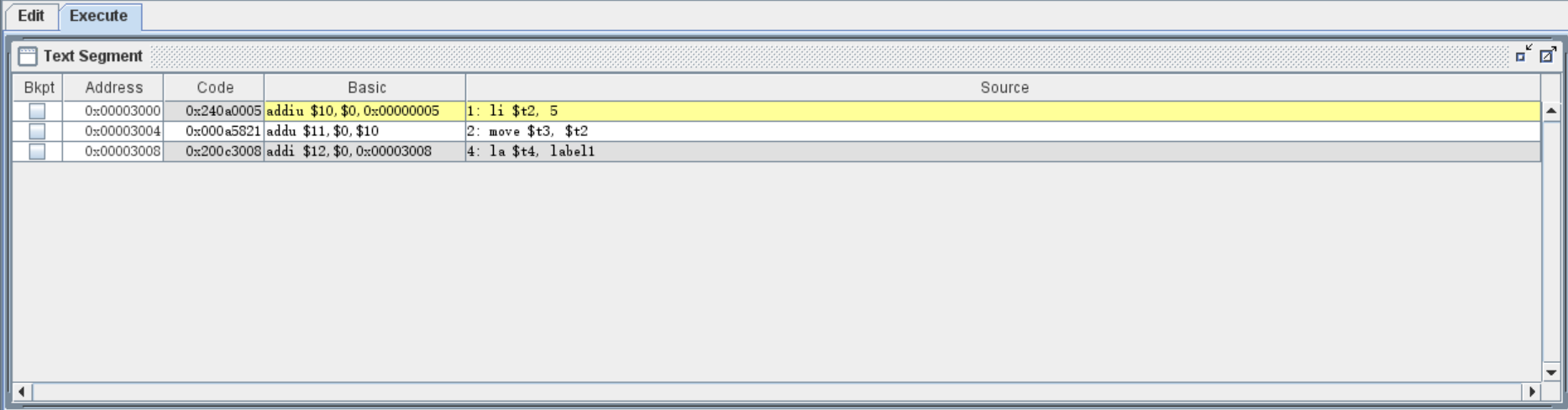
1 | j target |
在执行完 j target 之后,程序不会执行下一行的 li $t0, 1 ,而是会跳转到 target 标签的下方,执行下一条指令 li $t1, 2 。
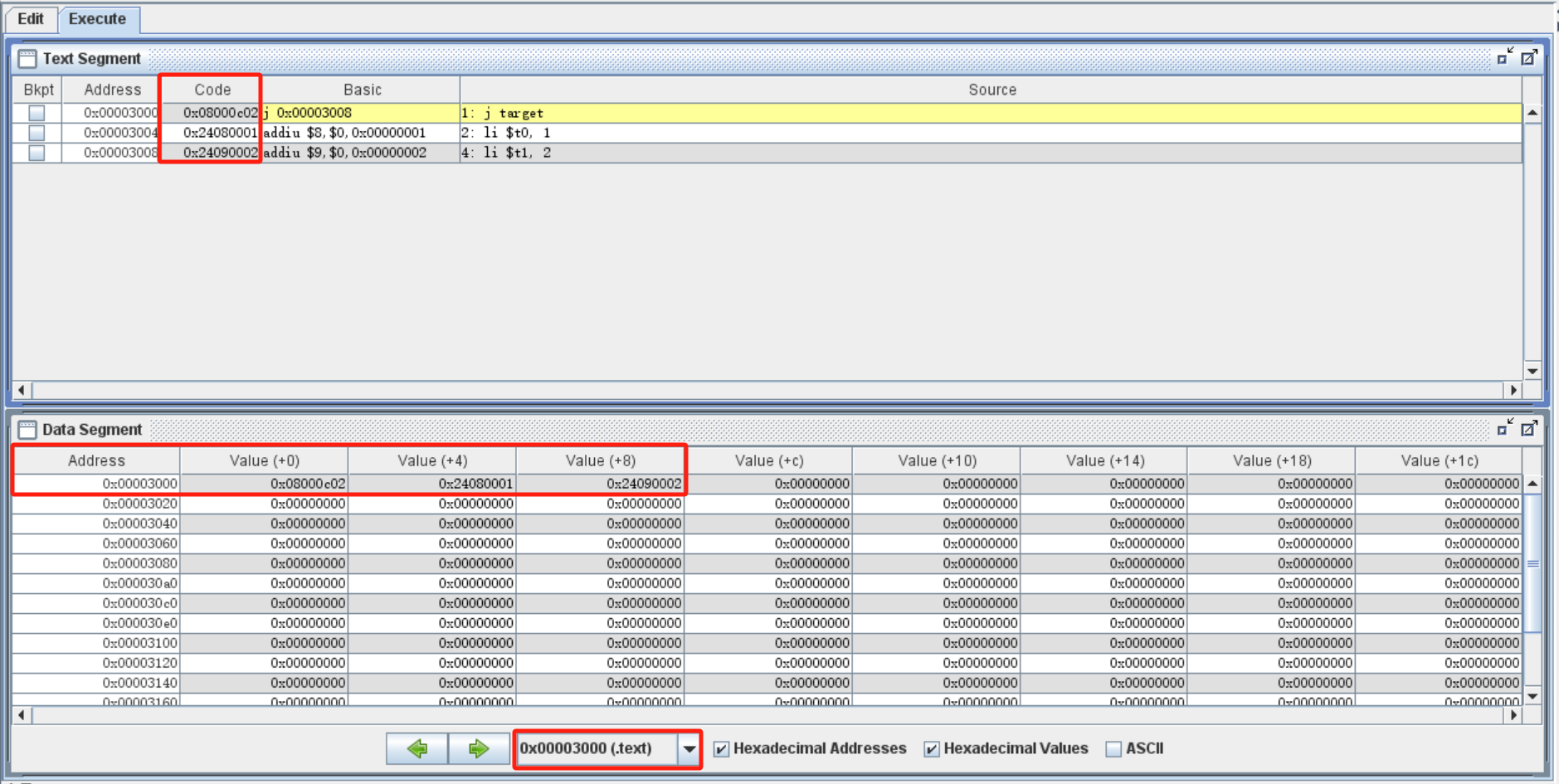
众所周知,一条指令中的标签 label 在 Execute 时会被翻译为一个立即数,那么 j 指令中的标签会被翻译为什么呢?我们执行一下上述代码,就可以看到 target 被翻译为了 0x00003008 ,而 li $t1, 2 这条指令对应的 Address 正好是这个数字:
其实,不仅我们使用 sw sh sb 指令写入内存的数据会保存在内存中,我们编写的每一条指令都会被转换为二进制码保存在内存中。前者占据了 0x00000000 到 0x00002fff 这一段地址,称为 .data 段;后者则占据 0x00003000 之后的地址,称为 .text 段。
我们在 Execute 界面中的内存界面,将下方的地址调整到 0x00003000 开始的 .text 段,就可以发现这一部分的内存已经被写入,而且写入的内容和上方每行代码的 Code 部分都不谋而合。这里的 Code 就是每条指令被转换为的二进制码,称为指令的机器码。在下一节我们将会具体学习每条机器码的含义,在这里我们只需要知道 MIPS 语言中的每条指令,转换为机器码都固定为 32 位,所以每条指令的地址 Address 也会按照顺序每条 +4 递增。
还是要提一下,j 指令不允许使用立即数作为参数,必须强制使用标签,我觉得可能是因为允许用户想跳到哪跳到哪还是太危险了()
接下来出场的是更强力的跳转工具,一对卧龙凤雏 jal 和 jr 。有的时候我们只是想短暂地离开,在执行完一段指令之后又希望能回到刚才离开的位置,这时候就需要用到这两条指令了。
jal 指令的用法和 j 指令一样,使用 jal label 即可跳转到 label 标签对应的位置。和 j 指令不同的是,jal 会把当前指令的下一条指令的地址写入 31 号寄存器 $ra 中。这个地址一般被称为 PC + 4 ,PC 指的当然就是当前指令的地址了,如果你向 MARS 右侧的寄存器界面下方看去,你就会发现真的有一个叫作 PC 的寄存器,在时刻保存着当前指令的地址。
jr 指令则用于返回跳转前的位置。使用 jr $ra 即可跳转至 jal 指令的下一条指令继续运行。注意在 jal 跳转到 jr 返回的这个过程中,千万不要篡改 $ra 寄存器的值,否则会跳转到乱七八糟的地方,不如说在任何过程中都不要随意篡改 $ra 的值,百害而无一利啊~
实际上我们也可以看出,jr 指令后面理论上可以接任何寄存器,它的作用只不过是将寄存器中的数据作为地址,跳转到地址所在的位置罢了,并不一定要与 jal 和 $ra 搭配,所以说也可以变相实现跳转至任意地址了。
其实这也解开了一个谜团,就是为什么 $ra 寄存器中保存的是 jal 指令的下一条指令的地址,而不是 jal 指令本身的地址。后者的话就会导致使用 jr 返回时再次执行 jal 指令跳转,从而就会导致死循环。
最后再介绍一下 jalr 指令,它实际上就是 jal 指令和 jr 指令的结合体。它跳转的方式和 jr 指令是一样的,都是跳转到寄存器所在的位置。另外,我们还需要再指定一个寄存器,用于将 PC + 4 存储在该寄存器中。例如指令 jalr $t1, $t0 ,就是跳转到 $t0 寄存器的值代表的地址,并将 jalr 指令的下一条指令的地址写入 $t1 寄存器中。
需要注意的是,jalr 指令后面的两个寄存器不能相同。如果说是为什么,主要是因为 jalr 指令执行时,是先将 PC + 4 写入寄存器,再执行跳转。如果两个寄存器相同的话,在跳转前寄存器的数据就会被覆盖掉,于是就没有办法执行跳转了。
【MIPS指令:相对跳转指令/条件跳转指令】 beq bne bgtz bgez bltz blez
接下来是条件跳转指令大家族,它们的特点是可以根据一定的条件选择是否进行跳转。相比寥寥数位的 j 型跳转指令,接下来的 b 型跳转指令真的可以算得上一个庞大的家族了。
首先是 beq 指令,它的全称是 branch if equal ,用法是 beq $t0, $t1, label 。当 $t0 的值等于 $t1 时,跳转到 label 标签所在的位置;否则不跳转。
相对的是 bne 指令,全称 branch if not equal ,用法是 bne $t0, $t1, label 。当 $t0 的值不等于 $t1 时,跳转到 label 标签所在的位置;否则不跳转。
有了等于和不等于,自然就有大小比较了,于是就有了 bgt(branch if greater than)、bge(branch if greater or equal)、blt(branch if less than)、ble(branch if less or equal)四条指令。以 bge $t0, $t1, label 举例,若 $t0 寄存器中的值大于等于 $t1 寄存器中的值,则跳转到 label 标签所在的位置;否则不跳转。
这时我们的警报又要响了,上一章的经验告诉我们,涉及到比较必须警惕有无符号的问题!上面四条指令都是有符号比较的指令,比如认为 0x1 大于 0xffffffff ,于是又有了这四条指令的无符号变种:bgtu bgeu bltu 和 bleu 。
有时我们经常需要将寄存器中的值和 0 进行比较,这时可以将指令中的第二个寄存器替换为 $0 ,不过我们还有更简单的选择,对于 beq bne bgt bge blt 和 ble 这六条指令,在后面加上字母 z ,变成 beqz bnez bgtz bgez bltz blez ,就可以表示和 0 进行比较,相应地,第二个寄存器参数就被取消掉了。例如 bgez $t0, label 指令,就表示如果 $t0 寄存器中的值大于等于 0 ,则跳转到 label 标签所在的位置;否则不跳转。
(你问我为什么 bgtu bgeu bltu bleu 后面不能加字母 z ?再仔细想想,你会为这个问题感到好笑的~)
刚才我们一口气学习了 16 条指令,看起来 b 家族真的是枝繁叶茂的大家族。然而对于精简的 MIPS 指令集来说,一切的繁荣都是虚假的,在它们之中其实只有 6 条指令是真指令,其余的竟然都是伪指令!这 6 条真指令就是 beq bne bgtz bgez bltz 和 blez ,不过其实并不需要太过区分,用起来都一样。
接下来,我们还是来关注一下 b 型跳转指令中的标签 label 被翻译成了什么,我们在 MARS 中输入如下指令:
1 | li $s0, 1 |
分析这一段指令,beq $s0, $s1, target3 语句的含义是比较 $s0 寄存器中的数据和 $s1 寄存器中的数据是否相等,如果相等,则跳转到 li $t7, 8 这条指令;否则继续执行 li $t6, 7 这条指令。
进入 Execute 界面,我们可以看到,标签 target3 并没有被翻译成 li $t7, 8 指令的地址 0x00003040 ,而是被翻译为了 0x00000001 !
实际上,b 型指令的标签翻译参考的是 跳转的目标指令 与 当前的 beq 指令的下一条指令 的相对条数。上面的例子中,标签对应的指令是当前 beq 指令后面的第二条指令,所以会被翻译为 0x00000001 。相应地,在上述指令中,如果标签 target3 对应的指令是 li $t6, 7 ,那么在 beq 指令中,target3 就会被翻译成 0x00000000 ;如果标签 target3 对应的指令是 beq 指令本身,那么就会被翻译成 0xffffffff(即 -1)。
这里要注意的是,标签的翻译代表的是相对的指令条数,而不是相对的地址,所以上述指令中 target 被翻译成 0x00000001 ,而不是 0x00000004 。
到这里,我们就已经学完了全部的跳转指令,现在你应该明白了为什么 j 型跳转指令被称为“绝对跳转指令”,而 b 型跳转指令被称为“相对跳转指令”了吧!
目前,我们已经学习了 MIPS 中最重要的三类操作:运算、访存和跳转。接下来要介绍的所有指令都离不开这三类操作,理解起来也会相对简单一些。我知道这一节可能有点太长了,不过前方就是胜利,加油吧!
【MIPS指令:位运算(2)】 sll srl sra sllv srlv srav lui
下面我们来学习 MIPS 中的左移和右移。MIPS 中的左移指令是 sll(shift left logical),使用 sll $t1, $t0, imm5 即可将 $t0 寄存器中的数据左移 imm5 位,存入 $t1 寄存器中。这里的 imm5 代表最高 5 位的立即数,也就是说左移的位数只能在 0 到 31 这个范围内选取,超出这个范围是没有办法执行的。
接下来就是右移了,通过上一章的学习,你一定知道了右移分为逻辑右移和算术右移两种。为了防止你忘记了,这里再简单介绍一下:逻辑右移时,高位一律补 0 ;算术右移时,需要根据原数据的正负确定高位补 0 还是补 1 。
在 MIPS 中,逻辑右移的指令是 srl(shift right logical),算术右移的指令是 sra(shift right arithmetic),用法和 sll 指令完全相同。
当我们进行乘除法时,如果乘数或除数是 2 的倍数,使用左移或右移就会比较便捷。例如如果要将 $t0 自乘 4 ,使用 mult 指令要用三步:li $t1, 4 mult $t0, $t1 mflo $t0 ,而使用 sll 指令则只需要一步:sll $t0, $t0, 2 ,非常地简单,非常地快速!
除了使用立即数作为移动位数以外,我们还可以使用寄存器中的值作为移动位数,这就需要用到 sllv srlv srav 指令了。在使用指令时,将 imm5 替换为寄存器即可。如 sllv $t1, $t0, $s0 ,就是将 $t0 寄存器中的数据左移 $s0 寄存器中的数据这些位,存入 $t1 寄存器中。
那么就又会出现一个问题,如果上述指令中的 $s0 寄存器中的值大于 31 ,该如何处理呢?或许你认为会报错,或是直接按封顶的 31 位去计算,但其实并非如此。答案是直接舍去 $s0 寄存器中的值的 5 - 31 位,只保留最低 5 位作为移动位数。所以如果 $s0 寄存器中的值为 0xf0 ,实际移动的位数就会是 0x10 ,即 16 位。
位运算部分的最后一条指令,就是 mario 的好兄弟 lui(load upper immediate)。其实在很久很久以前你就已经见过它了,只要涉及到向寄存器写入一个超大的立即数时,就会出现它的身影。
之前提过,ori 等指令中的立即数,位数最多为 16 位,超过 16 位就会变为伪指令。其实这是为了使每条指令的机器码都保持在 32 位的无奈之举,不然一个 32 位的立即数就把整个指令的空间占满了,其它信息实在是没有办法存进去,真的是太可怜了。
于是每当我们试图将一个高于 16 位的立即数写入寄存器时,实际上它都会分成两部分。先使用 lui 指令将高 16 位存入寄存器中,再使用 ori 指令写入低 16 位,真是非常天才的做法。
于是 lui 指令的功能就是将立即数左移 16 位之后写入寄存器,用法为 lui $t0, imm16 。例如 lui $t0, 0x1234 的结果就是向 $t0 寄存器中写入 0x12340000 。
【MIPS指令:条件赋值】 slt sltu slti sltiu
最后!最后!真的是最后了!我们来简单了解一下条件赋值指令。这几个指令真的就没什么存在感,但是考虑到后续设计 CPU 的时候要实现 slt 指令,所以就简单谈一谈,了解一下即可。
slt(set less than)指令的用法是 slt $t2, $t0, $t1 ,表示如果 $t0 寄存器中的值小于 $t1 寄存器中的值,那么就将 $t2 寄存器置为 1 。
当然,slt 的比较是有符号的比较,如果要无符号比较的话,就可以使用 sltu 指令,用法完全相同。
除此之外,这两个指令还有与立即数比较的版本,slti 指令的用法是 slti $t2, $t0, imm16 ,表示如果 $t0 寄存器中的值小于立即数 imm16 的值,那么就将 $t2 寄存器置为 1 。sltiu 指令也是同理。
和 b 型跳转指令相同,这 4 条指令也衍生出了巨量的伪指令,这里就简单罗列一下好了,相信聪明的你一定能猜出来它们的含义:seq sne sle sleu sgt sgtu sge sgeu 。你猜对了吗?
到这里我们就已经学完了 MIPS 所有的常用指令了!说多不多,其实无非就是我们之前提到的运算、访存、跳转三种类型。在接下来的教程中,我们就要开始实战,将之前学过的指令运用起来,同时也会接触到更多有趣的 MIPS 语法!
2.4 MIPS 编程实战
在这一节中,我们开始学习如何使用 MIPS 语言编写出一个完整的程序,以能够完美复刻出 C 语言的简单程序目标,开始训练吧!
【MIPS中的if分支】
首先我们来学习如何使用条件跳转指令实现 if 结构,以下面这段非常简单的 C 语言代码为例:
1 | if (a > b) { |
我们可以用下面这一段 MIPS 代码来实现它:
1 | bgt $s0, $s1, branch1 # $s0 = a, $s1 = b |
观察这段指令,我们将 if 替换为了 b 型跳转指令,指向第一个分支 branch1 ,将 else 替换为了 j 型跳转指令,指向第二个分支 branch2 ,成功实现了两个分支的分离。
另外我们还需要注意,在满足 a > b 的情况下,我们在分支的末尾加上了 j end 用来跳转到 branch2 分支结束处,否则在执行完 li $s0, 0 之后,就会继续执行 branch2 分支内的内容。
再提一点,由于汇编语言本身就十分抽象,为了在以后上百行的编写过程中不把自己绕晕,我个人建议还是保持要一个良好的代码风格为好。比如在变量定义和赋值时多写一些注释,再比如调整一下代码的缩进,尽可能和 C 语言的缩进相似,都是比较好的书写习惯。希望能够有帮助!
下一步我们再上一点强度,增加一个分支:
1 | if (a > b) { |
和简单分支一样,只需要加上一个 b 型跳转指令即可:
1 | bgt $s0, $s1, branch1 # $s0 = a, $s1 = b |
接下来,我们来练习一下带有逻辑运算符 && 和 || 的条件:
1 | if (a > b || b > c) { |
这里出现了逻辑或符号,那么我们应该如何应对呢?看下面这段指令:
1 | bgt $s0, $s1, branch1 # $s0 = a, $s1 = b |
从上面的代码可以看出,只需要连续两条条件跳转指令,将它们指向同一个分支,就可以表达出 || 的意思。那么如果是逻辑与呢?
1 | if (a > b && b > c) { |
这可能稍微有点麻烦了,因为只判断逻辑与一侧的表达式成立,并不能确定一个唯一的结果,不过你可能会想到这么操作一下:
1 | if (a <= b || b <= c) { |
这显然是一个相当不错的想法,能够极大地降低难度,如果只有 if - else 两个分支的情况下,我是非常建议你这么去做的!然而当中间再插入几个 else if 分支的话,这种做法就有点力不从心了。不过没关系,我们还可以这样修改我们的 C 代码:
1 | if (a > b) { |
这种嵌套的 if 结构就相当于在 branch 里面再加入一套 if 结构。听起来有点复杂,你可以先自己想想。绕出来了吗?看看下面的指令:
1 | bgt $s0, $s1, branch1 # $s0 = a, $s1 = b |
好了,我相信你已经对 if 结构有所了解了。感受到汇编语言的恐怖之处了吗?抓紧坐稳,我们继续发车:
【MIPS中的while循环、for循环】
要想实现 while 循环,我们依旧要借助条件跳转指令的力量。对于 while 循环,我有两种推荐的写法,你可以根据喜好选择一种,当然也可以根据不同情况灵活使用:
第一种是“进入循环时条件跳转,跳出循环时直接跳转”。例如下面这个 C 语言代码:
1 | a = 0; |
根据上面的描述,我们可以这样改写:
1 | li $s0, 0 # $s0 = a = 0 |
这种写法和刚才我们学过的 if 结构很像,优点是循环条件和 || 逻辑运算可以很好地结合,只需要再增加一个到 loop 的条件跳转即可,然而如果循环条件中出现 && 逻辑运算,写起来就会比较复杂。
第二种写法是“进入循环时不跳转,跳出循环时条件跳转”。以同一个例子为例,用这种写法写起来就会是这样:
1 | li $s0, 0 # $s0 = a = 0 |
显然这种方法的代码量比较小,而且也更像 C 语言中 while 循环的结构,然而缺点也显而易见,在跳转到 end 的条件跳转指令中,我们将 C 语言中的判断条件取了个反,变为了“如果 a >= 5 则跳转到 end 标签处”,如果是更为复杂的判断条件的话,有可能在取反这一过程中就出现错误了。
和前一种写法相对,这种写法的另一个优点就是循环条件和 && 逻辑运算可以很好地结合,同样只需要再增加一个到 end 的条件跳转即可。
我们接着再来说 for 循环,其实我们可以看出,刚才我们示例的 C 语言代码就是一个标准的 for 循环,我们可以将其改写成这样:
1 | for (a = 0; a < 5; a++) { |
我们知道,for 循环其实就是一种特殊的 while 循环。所以我们完全可以将每个 for 循环都拆解成 while 循环,按照 while 结构的思路完成我们的指令编写。具体改写方法其实就是三步:第一步,将括号中的第一部分提到循环的前面,在进入循环前为循环变量赋初始值;第二步,将括号中的第三部分放到大括号内的最后,在每一次循环结束之后更新循环变量的值;第三步,把 for 改为 while 就可以了。
比如对于下面这两段 C 语言代码,第一段中的 for 循环与第二段中的 while 循环就是等价的:
1 | if (n % 2 == 0) { |
1 | if (n % 2 == 0) { |
(这是一段简单的判断一个数是否是质数的代码,如果你没看出来的话,那简直是太可怕了)
【MIPS中的数组】
在掌握了基本的语法之后,我们就来学习一下如何存储大量的数据。在编程时,我们难免会遇到需要存储一系列大量数据的情况,这时候我们肯定是不能为每个数据都创建一个变量了。在 C 语言中,我们可以使用数组、链表等各种各样的形式来存储这些数据;在更低级的 MIPS 中,我们就选择将这些数据存入内存中。接下来我们就来学习如何通过内存模拟数组的定义与存取。
还记得我们在上一节讲过的有关“段”的内容吗?.data 段指的是地址为 0x00000000 到 0x00002fff 的一部分内存,我们可以随意使用这个段中的内存来存储大量数据;.text 段指的是地址为 0x00003000 之后的内存,这一段用来存储我们的 MIPS 指令的机器码。
于是我们就可以在 .data 段中开辟出一块连续的空间,用来作为数组存储一系列的大量数据。如下面一段指令所示:
1 |
|
(在编写指令时,写入的段默认为 .text 段,如果要切换写入的段,则需要像上述指令中一样,使用 .data .text 等进行切换)
我们首先输入 .data ,证明我们接下来要在这个段中开辟空间。在接下来的每一行中,我们先写上我们自定义的数组名,在英文冒号后加上 .space ,后面接上我们要开辟的空间的字节数。这里我们为 array1 数组开辟了 20 个字节的空间,但是要注意这个数组的大小不是 20 ,因为我们要存储的每个数据都要占据 4 个字节的空间(哪怕是只占据 1 字节的 char 型数据也建议直接用 4 字节来存储,我们的内存足够多,不需要担心不够用,使用 4 字节存储和寄存器的位数一致,也可以非常方便地使用 sw 和 lw 指令直接进行存取,也可以降低出错的概率,这个括号真的好长啊~),所以这个数组实际上只能存储 5 个值,即从 array1[0] 到 array1[4] ;同理,array2 数组开辟了 40 个字节的空间,能够存储 10 个值,从 array2[0] 到 array2[9] 。
在向数组进行存取时,我们使用内存访存指令 sw 和 lw 就可以实现。这里的 array1 和 array2 可以作为标签 label 来使用,我们都知道标签在运行时会被翻译成立即数,实际上这两个标签代表的是两个开辟出的空间的首地址。对于 array1 数组来说,标签 array1 代表的立即数就是 0x00000000 ,因为空间是从 .data 段的首地址 0x00000000 开始分配的;对于 array2 数组,标签 array2 代表的立即数就是 0x00000014 ,也就是十进制的 20 。因为 array1 占据了地址为 0x00000000 到 0x00000013 的空间,array2 就顺延下来进行分配了。
如果要我来说的话,这种顺延下来的分配其实是一种特别坏的设定。比如在这个例子中,一旦 array1 申请的字节数不能被 4 整除,array2 的首地址就同样会不能被 4 整除,导致我们用 sw array2($0) 等指令进行数组的读写操作时,程序会因为 sw 要访问的地址不能被 4 整除而直接报错崩掉。所以说,我们最好保证在申请数组时,申请的字节数永远都能够被 4 整除!
接下来我们再谈谈内存访存指令中括号部分的内容。首先要注意的是括号里的内容应该是一个寄存器,而不是立即数,这一点在最开始讲内存访存指令的时候就已经强调过了。
还有一点要注意的就是,寄存器中的值不是数组的下标,而应该是数组下标乘 4 的结果。为了简便计算,我们经常会使用位运算来计算乘 4 的结果,比如使用 sll $t1, $t0, 2 就可以将 $t0 寄存器中的值乘 4 写入 $t1 寄存器中了。
接下来我们来学习一下二维数组。早在学习 C 语言时,你可能就听说过,C 语言中的二维数组其实就是一维数组的一种简单写法,二维数组在存储时其实是按行展平之后再存储的。我们接下来就要用到这种思路来实现二维数组。
例如我打算开辟一个 3 行 5 列的数组,于是我需要申请一个 3 * 5 * 4 = 60 字节的内存(你自己写时可以开大一点,防止自己算错空间导致溢出)。这一步还是比较好算的,关键在于如何正确对二维数组进行读写。
我们知道,二维数组在存储时会按行展平成一维数组,也就是按照第一行、第二行、第三行……的顺序紧密排列进行存储的。例如在一个 m 行 n 列的二维数组 matrix 中,matrix[i][j] 实际上和 matrix[i * n + j] 是相同的,于是 i * n + j 的值再乘 4 ,其实就是读写二维数组时,括号中的寄存器的值。
可想而知,每次对二维数组进行读写时,如果我们拿着两个数组下标,想要求出括号中的寄存器的值,还是比较复杂的,例如在刚才的 3 行 5 列数组 matrix 中,使用两个数组下标写入 matrix[1][2] 这个元素,就需要进行下面一通操作:
1 |
|
确实很复杂,但是我们在之后会讲到宏,使用宏可以将计算过程提取出来,避免重复造轮子。除此之外,我们还可以进行一点小优化,那就是在申请空间时,将二维数组的列数扩展到 2 的幂次,这样就可以不使用 mult 指令进行计算,而是使用位运算指令 sll 一步到位了!例如在这个例子里,我们就可以申请一个 matrix[3][8] 的数组,大小为 96 字节。在使用这个数组时,第 0 到 4 列正常使用,第 5 到 7 列直接不理它就好了。
学习了二维数组的用法,相信你也已经能够举一反三,写出更高维数组了!(虽然我估计也不会用到)快去尝试一下吧!
【MIPS中的字符、字符串】
在 MIPS 中如何表示字符?你肯定猜到了,当然是使用字符的 ASCII 码值了。我们知道,ASCII 码值的范围是 0 到 127 ,也就是说,最多使用 7 位二进制数就能够表示出我们常用的所有字符。出于方便,我们使用一个字节(8 位)来表示一个字符,和 C 语言中 char 型变量的大小完全相同。
(如果你好奇 ASCII 码值为 128 到 255 的字符被定义为了什么,可以上网查一下,都是一些键盘上打不出来的特殊字符)
我知道你会觉得很简单,不过这一部分真的很容易搞混,因为十六进制的 ASCII 码和字符本身长得完全一样。还记得我之前想要输出字母 b ,于是在寄存器里写入了 0x0000000b ,结果输出不出来任何东西,我还以为是 MARS 的 bug 。实际上,0x0000000b 代表的是 \v ,一种空白符号,当然没有输出了,而真正表示字符 b 的应该是 0x0x00000062(晕)!
接下来我们来谈谈字符串。如果要存储字符串的话,我们就很难使用寄存器了,毕竟一个寄存器只能存放 4 个字符。所以我们可以将字符串写入内存中。
和上一部分的数组一样,我们也可以通过在 .data 段作出声明的形式来把字符串写入内存中。像下面这样:
1 |
|
我们执行这段指令,就可以在下方的内存界面处看到我们写入的内容。不过此时的内容还是十六进制的形式,我们可以点击下方的 ASCII 来将每个字节的内容转换为字符形式:
我们可以观察一下这些字符的排列顺序,这些字符的顺序看上去似乎混乱不堪,但再仔细观察一下就可以发现,这些字符其实都是按照地址从低到高排列的。我们之所以觉得混乱,是因为在每个字中,4 个字节的地址是从左往右越来越低;而字与字之间的排列顺序,则是从左往右地址越来越高。假如在第一个字中,l l e H 的地址分别是 0x3 0x2 0x1 0x0 ,按照地址从低到高来读正好是 H e l l ;第二字中的 W (空格) , o 的地址分别是 0x7 0x6 0x5 0x4 ,按照地址从低到高来读是 o , (空格) W 。像这样依次读下去,就能够得到我们写入的字符串了。
你肯定已经发现了,在上面的指令中我使用了两种声明的形式,一种是使用 .ascii 来声明,一种是使用 .asciiz 来声明,那么你发现这两种声明方式的区别了吗?
答案就藏在字符串的尾部。我们可以发现,使用 .ascii 声明的字符串 Hello, 的后面直接接了下一个字符串的首字符 W ,而使用 .asciiz 声明的字符串 World! 的后面接了一个 \0 之后,接着才是下一个字符串的内容。二者的区别就在于结尾的这个 \0 。
和 C 语言一样,MIPS 中的字符串也是要以 \0 结尾的,如果一个字符串的结尾没有 \0 ,那么它就会和后面的内容连成一个字符串,直到遇见 \0 为止。如果你没太懂,那也不要紧,在下一部分 syscall 的内容中,我们还会再深入讨论这个问题~
最后还想强调一点,在之后我们经常会遇到在 .data 段要同时声明数组和字符串的情况,请记住一定要先声明数组,再声明字符串!道理其实很简单,因为如果先声明字符串的话,如果字符串的字节数不能被 4 整除,数组的首地址就又跑到不能被 4 整除的地方去了(叹气)。
【syscall:输入、输出、结束运行】
讲到这里,你会发现一个非常有趣的问题,那就是我们竟然还没有讲如何输入和输出数据!虽然我们一直在试图模仿当年学习 C 语言的过程来学习 MIPS ,但是想当年我们可是在第一节课就学了 scanf() printf() 这些函数的用法,然而现在我们却一直在回避输入输出的问题,这不可疑吗?
很遗憾,确实是这样的。事实上,对于在 CPU 上运行的汇编语言来说,要想仅通过自身来实现某些功能,是完全不可能的,哪怕是从外部输入和向外部输出这么简单的功能。正因为这两个功能需要通过与外部进行交互来实现,所以我们的汇编语言拿它们完全是束手无策,这时候就需要系统调用 syscall 来进行支援了!
因为在操作系统课程中我们才需要具体学习系统调用的相关知识,在这里就不详细介绍了。简单地来说,系统调用其实就是一些“求救信号”,当我们遇到一些没有办法实现的需求时,就可以喊出万能的 syscall ,召唤神奇的操作系统,来帮助我们解决问题。至于具体是怎么解决的,起码我们现在不需要知道,只需要快乐地 syscall 就 OK 了~
(相信我,操作系统这门课,一学一个不吱声,所有人都内核崩溃了)
众所周知,系统调用 syscall 肯定不止一种,那么我们该用什么方法来区分不同的 syscall 呢?答案是使用当前 $v0 寄存器中的值。也就是说,在我们使用 syscall 指令时,CPU 会根据当前 $v0 寄存器中的值,来判断执行哪种系统调用。
我们在 MARS 中按 F1 查看帮助,在 Syscalls 一栏中即可查看系统调用的种类和它们对应的 $v0 值。(当然,其它栏中的内容也非常有用,有时间的话可以仔细研读一下)
我们在 Syscalls 一栏中往下翻,找到 Table of Available Services ,这个表格中有好几十种系统调用,看得人眼花缭乱,但是我们只需要学其中的几种就可以了(开心)。
| Service | Code in $v0 | Arguments | Result |
|---|---|---|---|
| print integer | 1 | $a0 = integer to print | |
| print string | 4 | $a0 = address of null-terminated string to print | |
| read integer | 5 | $v0 contains integer read | |
| exit (terminate execution) | 10 | ||
| print character | 11 | $a0 = character to print | See note below table |
| read character | 12 | $v0 contains character read |
Service 11 - Prints ASCII character corresponding to contents of low-order byte.
print integer ,也就是输出一个 int 型整数,在系统调用前需要将 $v0 寄存器的值置为 1 。Arguments 一栏指的是系统调用时需要提供的参数,也就是说我们需要把要输出的整数事先写入 $a0 寄存器中。例如下面一段指令:
1 | li $a0, 114514 |
我们在 MARS 中运行这段指令,在下方的交互界面中点击 Run I/O 选项,就可以看到下方输出了十进制的 114514 :
read integer ,也就是输入一个 int 型整数,在系统调用前需要将 $v0 寄存器的值置为 5 。Result 一栏指的是系统调用的结果,从描述中可以看出,输入的 int 型整数存储在 $v0 寄存器中。也就是下面这段指令:
1 | li $v0, 5 |
同样,在 MARS 中运行这段指令,我们就会发现程序运行时停在了第一个 syscall 这一行。我们在下方的交互界面中输入一个十进制数字,再按下回车,我们刚才输入的数字就会以十六进制的形式存入 $v0 寄存器中。例如输入 114514 ,$v0 寄存器的值就会变为 0x0001bf52 。
需要注意的是,此时 $v0 寄存器中的值发生了改变,于是我们在每次输入时都需要为 $v0 寄存器重新赋值。
此外,我们还要注意两个系统调用使用的寄存器是有所不同的,输出时要输出的整数存储在 $a0 寄存器中,输入时被输入的整数存储在 $v0 寄存器中,这一点千万不要忘了!顺带一提,如果考试的时候忘记了,别忘了还可以按 F1 ,找到上面的表格来查看一下哦~
print character 和 read character 的用法和上面两个系统调用就非常相似了,只不过把输入输出的内容从 int 型改为了 char 型,$v0 寄存器的值不同而已,流程其实都是一样的。另外要注意的是,字符只占一个字节,所以在输出字符时 $a0 寄存器的值只有最低 8 位是有效的,剩下的高位会被忽略掉。
然而在输出字符串时,流程就有所不同了。和前两个输出不同的是,输出字符串时 $a0 寄存器内的值并不是我们要输出的内容,而是要输出的字符串的首地址。输出时会从首地址所在的字符开始不停输出,直到遇到第一个 \0 字符为止。
那么我们该如何将 $a0 赋值为字符串首地址呢?这时候就要请出我们的古神 la 指令了!字符串的名字同样也是标签,于是我们就可以使用 la $a0, label 将标签对应的值,即字符串首地址赋给 $a0 寄存器。
我们再拿上一部分中的三条指令作例子,当我们使用下面的指令时,三次 syscall 指令输出的结果是什么呢?
1 |
|
答案分别是:Hello, World! ello, World! 和 World! 。你答对了吗?
在输出 str1 时,因为 str1 使用的是 .ascii ,结尾没有 \0 ,所以会一直输出到 str2 结尾的 \0 才结束。随后,我们将 $a0 寄存器的值自增 1 ,此时 $a0 寄存器指向的地址就从 Hello, 中的 H 转移到了 e ,所以从 e 开始输出。在输出 str2 时,因为 str 使用了 .asciiz ,结尾有 \0 ,所以直接输出了 str2 的内容。
这个故事告诉我们,没事不要乱用 .ascii ,正常用有 \0 结尾的 .asciiz 就好……
实战中我们也经常将单个字符使用字符串的形式来存储,例如空格 " " 和换行符 "\n" ,然后使用输出字符串的方法来输出。把这些符号放进内存里,可以把寄存器节省下来,毕竟一共就那么几个寄存器,真的很宝贵:
1 |
|
最后就是结束运行的系统调用了,和 C 语言在 main() 函数中执行 return 0 一样,执行这个系统调用会让程序直接停止运行。调用方法就比较简单了,只需要将 $v0 寄存器的值置为 10 ,再执行 syscall 就可以了。
在我的印象里,官方的指导书里貌似提到过,如果 MIPS 程序结尾不使用这种方法结束运行,在评测机上好像会出现错误,所以还是尽量给每个程序都加上结束吧(摊手)~
【MIPS中的宏定义】
到目前为止,相信你已经充分体验到了使用 MIPS 进行编程的复杂,有时候哪怕非常简单的一个功能,用汇编语言实现起来都可能需要上百行。那么,有没有什么压缩指令条数的方法呢?
有的兄弟,有的!使用宏定义,我们就可以将几条重复或相似的语句合成成一条语句了!
来看这个例子,我们使用 .macro 和 .end_macro 定义了宏 exit ,在 .text 段编写指令时,我们就可以使用 exit 来代替宏定义中的两条指令:
1 | exit # or .macro exit() |
可以看到,我们在 .macro 的后面写上了宏的名称 exit ,然后在下方写上结束运行的指令,最后以 .end_macro 结尾,就完成了宏定义的编写。调用时只需要使用宏名 exit 调用即可。(这里因为宏没有参数,所以在定义和调用时,后面加不加括号均可)
刚才我们提到了宏的参数,正是这样,我们还可以使用 % + 自定义参数名 的方式为宏添加参数,比如下面这个例子:
1 | push(%d) |
这一段指令就是我们在稍后会讲到的压栈和弹出指令。通过这一段指令,我们就可以实现将 $t0 寄存器和 $t1 寄存器中的值压入栈中,再以先进后出的规则将它们弹出的过程。
实际上,在这段指令被执行前,带有宏的指令会被展开成正常指令。例如 push($t0) 这行指令,在展开时将 $t0 这个参数代入到宏定义 push(%d) 中 %d 的位置,替代其中两行代码中所有的 %d ,于是 push($t0) 就被转换为了下面两行指令:
1 | addi $sp, $sp, -4 |
根据这个规则,上述代码就会被转换成这样的 10 行指令:
1 | addi $sp, $sp, -4 |
除了我们经常会用到的压栈和弹出指令以外,我们还可以将输入和输出指令打包成宏来使用:
1 | scanfint(%addr) |
此外,宏不仅可以有一个参数,使用逗号分割,我们就可以使用多个参数:
1 | getoffset(%ans, %i, %j) |
这里的 getoffset 宏的作用是,计算每行 8 列的二维数组中第 %i 行第 %j 列元素的地址,相对于该二维数组首地址的偏移值。在二维数组相关的题目中,我们也会经常用到这个宏。
刚才我们提到的这些宏,基本上就是我们在以后的学习中比较常用的所有宏了。接下来我将为你介绍一些更神奇的宏的特性,助你玩转宏定义!(说不定在下一部分中还有妙用哦!)
事实上,宏中带 % 的自定义参数不仅能够表示某个寄存器,它甚至可以表示一条指令中的任何一个部分,比如立即数:
1 | para(%p) |
还有标签:
1 | label(%l) |
令人不可思议的是,它甚至可以表示指令名:
1 | instr(%i) |
(不过如果输入的指令名不满足上述格式就会直接报错了)
不仅如此,宏还支持在自身内部跳转:
1 | branch(%d) |
当然,如果你试图从外部跳转到宏内,或者从宏内跳转到外部的话,就没办法通过编译了……
或许你还没有 get 到宏内部跳转的神奇之处,那么我们试想一下,在上面的指令中,如果我们直接将宏展开,会发生什么问题?答案是 iszero 和 end 标签就会出现两次,整个程序就没办法运行了!
我们来运行一下这个程序,看看 MARS 展开的宏是什么样的:
我们可以发现,MARS 聪明地将两个标签加上了后缀,用以区分不同标签,真的是太细了!
除此之外,宏甚至还支持嵌套调用:
1 | para(%p) |
当然,如果宏自己调用自己,或者出现了循环调用(比如宏 para 调用宏 instr ,而宏 instr 又调用宏 para ),就没有办法展开了……
真是万能的宏,让我们歌颂宏!
【MIPS中的函数、递归函数、栈】
最后,我们再来学习一下 C 语言转 MIPS 语言中函数的写法。我们来看这一段代码:
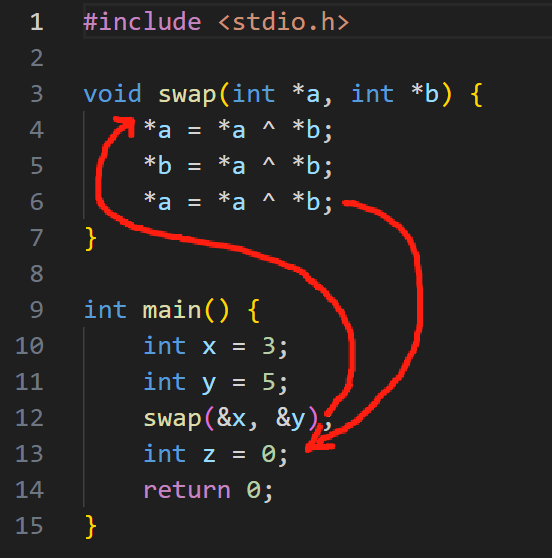
1 | void swap(int *a, int *b) { |
这是一个非常经典的交换函数,根据我们现有的知识,我们该如何在 MIPS 中实现相同的功能呢?
或许你已经想到了一个非常巧妙的办法,我直接把函数展开,不调用函数不就可以了吗?像下面这样:
1 | int x = 3; |
于是就可以写成下面的 MIPS 指令:
1 | li $s0, 3 # $s0 = x = 3 |
非常聪明的解法!事实上,在我们亲自去进行 MIPS 编程时,当我们遇到这种比较简单的函数时,我也推荐大家使用这种方法,也就是非必要尽量不创造函数,而是直接将其展开到主函数中。
那么,如果这个函数的调用次数特别多呢?例如,我现在要对 10 对不同的寄存器分别执行交换操作,怎么样才能使我们的指令更加简洁呢?这时候就可以使用我们刚才学过的宏定义:
1 | swap(%var1, %var2) |
如果函数有返回值呢?我们有两种解决方法。第一种就是将存储返回值的寄存器作为一个参数,写在宏定义中。当函数有返回值,但我们并不需要它时,我们也可以在使用宏时,将存储返回值的寄存器设为 $0(还记得吗?$0 寄存器的值永远为 0 ):
1 | myadd(%var1, %var2, %res) |
第二种方法就是将所有函数的返回值都固定存储在一个寄存器中(如 $v0 寄存器),在调用结束之后,使用 move 指令将存储返回值的寄存器转移到其它寄存器中:
1 | myadd(%var1, %var2) |
对于一般的函数,我们使用宏基本上就完全可以实现翻译了,真是太美妙了!然而,对于一种特殊的函数,我们却束手无策,那就是递归函数!
其实你也应该猜到了,在真实的编译过程中,函数绝对不是通过像宏定义一样直接展开到指令中来实现的,而是跳转到一段指令中,执行结束之后再跳转回原来的位置。就像下图这样:
看到这张图,你可以试着想象一下它对应的指令是什么。这是你或许就会产生一个问题了,我们可以在程序的任意位置调用这个函数(甚至是这个函数自身内部),那么我们该如何实现函数执行结束后跳转回原来的位置呢?这就要请出我们好久不见的老朋友:jal 和 jr 了!
我们知道,jal 指令和 j 指令的不同之处就是,jal 指令在执行跳转的时候,会将当前指令的下一条指令的地址保存在 $ra(即 $31 )寄存器中。而 jr 可以跳转到任意寄存器的值代表的地址处。于是,我们只需要在调用函数时,将 j 指令替换为 jal 指令,在返回时使用 jr $ra ,就可以实现上面图中的过程了。
或许你还会问,那函数的参数和返回值怎么办呢?我们手写的函数没有办法像宏那样直接传参,不过我们可以借鉴一下刚才使用宏实现函数时,对返回值处理的办法。
我们之前提到的两种方法中,有一种方法就是将函数的结果统一写入一个固定的寄存器中(比如 $v0 寄存器),再在调用宏结束之后统一 move 到其它寄存器中,我们在这种函数的写法中也可以使用这种方式来传递返回值。
其实参数也是同理,我们可以在调用函数前,将参数统一装入一些固定的寄存器内,调用时直接取用即可。一般来说,我们约定俗成的参数寄存器是 $a0 $a1 $a2 $a3 这四个寄存器,分别存储函数的第 1、2、3、4 个参数。什么?你问我如果参数超过 4 个该怎么办?如果这是操作系统课程的话,我肯定会教你将多出来的参数压栈,还会告诉你在栈中要留出前 4 个参数的虚空位置等等……但这里是我们堂堂 CO 课程!我会告诉你,从别的寄存器那里偷几个来用不就好了嘛(笑)!
还是这段比较经典的 C 语言代码:
1 | int myadd(int a, int b) { |
于是我们就可以这样翻译:
1 | li $s0, 3 # $s0 = x = 3 |
像这样,我们就用非常标准的方法完成了函数的翻译!那么接下来,我们来挑战一下递归函数吧!考虑下面这个 C 语言代码:
1 | int gcd(int a, int b) { |
这是一段求两个正整数的最大公因数的代码,如果你直接套用刚才的模板,就会得到这样的程序:
1 | # warning: this code is wrong, don't learn this!!! |
(再次提醒,这段代码是完全错误的,请不要学习这段代码!!!好吧虽然有点剧透了,但我还是要强调再强调)
你现在已经为自己能够完成这么复杂的一个 MIPS 程序而沾沾自喜了,对吗?很抱歉,我要泼你一盆冷水了。你可以试着运行一下这段代码,就会发现它在 jr $ra 这行指令处出现了死循环。这是为什么呢?
揭晓答案!我们知道,每当我们调用一次 jal 指令时,$ra 中都会被写入当前指令的下一条指令的地址。于是,当我们在 gcd() 函数中再次调用 gcd() 函数时,$ra 中的地址就会被新地址覆盖掉,以此类推。导致最后真正要返回时,我们只能返回到最后一次调用 gcd() 函数的位置,而没有办法实现我们预想中不断跳出的结果。如果你还是不太明白,可以试着在运行上述错误代码的同时,观察 $ra 寄存器中的值的变化,或许你会对这个问题有更直观的理解。
如果类比 C 语言的话,寄存器就像是 C 语言中的全局变量。和作用域为函数内部的局部变量不同,所有的函数都共享着同一个 $ra 寄存器,只要有一个函数修改了它的值,所有函数的返回地址都会随之改变。
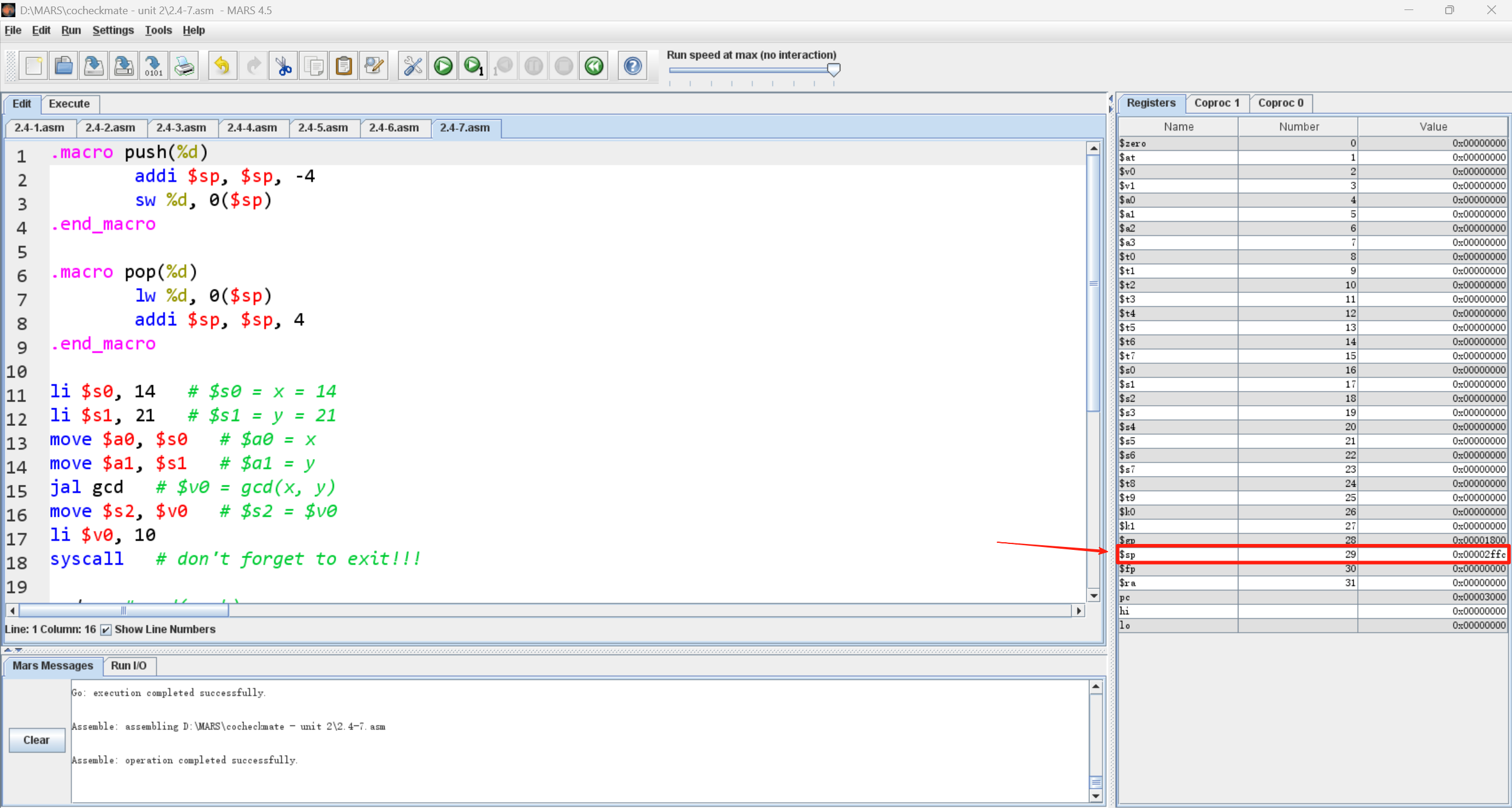
那么,为了解决这个问题,我们该如何将函数的返回地址保存下来呢?这里就需要用到栈了。
观察 MARS 界面右下角的寄存器界面,我们能够找到一个名为 $sp 的寄存器,它就是栈寄存器。我们可以发现,和大多数寄存器不一样,它的初始值不是 0 ,而是 0x00002ffc :
看到这个初始值,你可能就会联想到 .data 段的范围正是 0x00000000 到 0x00002fff 。没错,栈寄存器的初始值确实与此有关,它的值实际上就是 .data 段上最后一个字(32 位)空间的首地址。
在操作系统中,栈空间其实是一个自顶向下的空间。也就是说,当我们将寄存器中的值压入栈中时,栈寄存器 $sp 的值会减少 4 ,随后将寄存器中的值写入当前 $sp 寄存器的值代表的地址中;当我们想将栈顶的数据弹出到寄存器中时,需要先将当前 $sp 寄存器的值代表的地址中的数据读取到寄存器中,再将 $sp 的值增加 4 。听起来非常拗口,实际上就是下面的过程:
以 $s0 寄存器为例,将其中的数据压入栈时,实际上就是执行这两条指令:
1 | addi $sp, $sp, -4 |
(注意这里的 sw $s0, 0($sp) 指令完全不等于 move $s0, $sp 指令,原因在最开始讲内存访存指令时提到过,如果你还讲不清楚它们为什么不相等的话,赶紧回去恶补一下吧!)
将栈顶的数据弹出到 $s0 寄存器,实际上就是执行这两条指令:
1 | lw $s0, 0($sp) |
这样,我们就实现了把寄存器中的值暂存下来,防止寄存器中的值丢失的效果。那么,我们应该在什么时候压栈,又应该在什么时候弹出呢?有两种比较经典的做法:
一种做法是在调用函数之前压栈,在函数返回之后弹出,像下面这样:
1 | push(%d) |
另一种做法是在刚进入函数时压栈,在函数即将返回时弹出,像下面这样:
1 | push(%d) |
其实两种写法的作用是等价的,就像有的人喜欢饭前饭后刷牙,有的人喜欢起床后和上床前刷牙一样。我个人比较喜欢后者的写法,因为一个函数可能被调用很多次,每次调用的时候都需要在两侧压栈和弹出;而函数本体总归是只有一个,所以只需要写一次压栈和弹出即可。(这个道理放在刷牙的例子上也很直观,真是个好例子!不过真的有人饭前刷牙吗?)
不仅是 $ra 寄存器,所有的寄存器都不例外。只要递归函数中使用了某个寄存器,随后调用了自身进行递归,在调用结束返回之后继续使用这个寄存器,同样会出现刚才的数据覆盖问题。另外,在非递归函数中,我们也经常会将一些函数中用不到的数据先压入栈中,腾出寄存器的位置来,防止寄存器用光,等到函数运行结束返回之前,再从栈中弹出寄存器的值。
在向从栈中弹出的过程时,我们一定要注意栈结构先进后出的原则,千万千万不要把弹出的顺序搞反,否则整个程序就混乱不堪了!
1 | push(%d) |
所以到这里,你应该已经能驾驭递归函数了。现在试着改一改刚才求最大公因数的程序吧!真的很简单:
1 | push(%d) |
2.5 MIPS 机器码
在上一节中我们已经了解到,我们学习的 MIPS 中每条指令都会以 32 位机器码的形式存储于 .text 段中,或许你也会好奇它们之间是如何转换的,下面我们就来学习一下 MIPS 的基本原理 ——
【J型指令】
我们首先来认识一种最简单的指令:J 型指令。J 型指令的特点是,指令的参数中没有任何寄存器,只有一个立即数,例如我们之前学过的 j 和 jal 指令。(别忘了,标签和立即数在翻译成机器码时是等价的!)
J 型指令的 32 为机器码结构十分简单,一共只有两个部分:31 到 26 位代表指令的名称(例如 000010 代表 j 指令,000011 代表 jal 指令),称之为 OpCode ;25 到 0 位代表 26 位的立即数。
| 31..26 | 25..0 |
|---|---|
| OpCode | imm26 |
下面我们来通过一个例子,看 J 型 MIPS 指令是如何转换为机器码的:假设有一条地址为 0x00003004 的指令 j target ,其中 target 是一个标签,指向地址为 0x0000301c 的指令。
这条指令的机器码为 0x08000c07 。注意这是十六进制的编码,我们在将其拆分的时候一定要保持谨慎,实在不行就把它转换成二进制再拆分,也算是一种比较稳妥的方法。
首先我们来看它的高 6 位,为 0x02 ,也就是 0b000010 ,代表着 j 指令。其次是低 26 位,为 0x0000c07 ,实际上它是 0x3004 右移两位之后的结果。至于这里为什么要右移两位呢,这就涉及到 MIPS 机器码中立即数的扩展了,我们稍后会再讲到。总而言之,将上面的两部分合起来,就能够得到 32 位的机器码了!
【I型指令】
接下来我们来了解一下 I 型指令。绝大多数含有立即数的指令都是 I 型指令,我们常见的有:所有的内存访存指令(如 lb sb 等)、相对跳转指令(如 beq bne bgtz 等)和除移位运算以外的带有立即数的运算指令(如 ori addi sltiu lui 等)。简单来说就是 6 个内存访存指令,以及所有 b 家族和 i 家族的指令都是 I 型指令(当然了,sub mfhi 这种 b 和 i 就别来攀亲戚了,笑)。
I 型指令由四部分组成,31 到 26 位(OpCode)同样代表指令的名称;25 到 21 位为第一个寄存器的编号(0 到 31),称为 rs 寄存器;20 到 16 位为第二个寄存器的编号,称为 rt 寄存器;15 到 0 位代表 16 位的立即数。
| 31..26 | 25..21 | 20..16 | 15..0 |
|---|---|---|---|
| OpCode | rs | rt | imm16 |
这里要注意的是,虽然机器码中寄存器和立即数的顺序是这样的,但这并不意味着指令中它们的顺序也是这样。b 家族的指令谨遵指示,指令形如 beq rs, rt, label ,label 即是 imm16 ,于是 b 家族的指令和机器码的顺序一模一样;i 家族有些叛逆,指令形如 ori rt, rs, imm16 ,其中的 rt 和 rs 位置正好相反;内存访存家族最为放荡不羁,指令形如 sw rt, imm16(rs) 或 sw rt, label(rs) ,整个顺序都被弄得乱七八糟,真的是搞得人非常头大。
(这里打个补丁,beq 和 bne 指令的结构确实如上述所说,但 bltz blez bgtz bgez 指令中只有一个寄存器,形如 blez rs, imm16 。其中 blez bgtz 指令的 rt 为 00000 ;而 bltz bgez 指令的 OpCode 相同,均为 000001 ,区别在于前者的 rt 为 00000 ,而后者的 rt 为 00001 。我不知道为什么要这样设计,简直太邪门了,不过还好我们以后应该不需要实现这四条指令,也不用把这件事太放在心上~)
其实有一个简单的规律,不知道你有没有发现,在 MIPS 指令的书写中,如果一条指令涉及到给某个寄存器赋值,那么这个寄存器就一定会被写在最前面,例如我们刚才提到的 i 家族指令和内存访存指令。而在 I 型指令中,如果有寄存器被赋值,那么它就必然是 rt 寄存器,rs 寄存器不具有被赋值的功能。(当然,后面的上机考试中,有些助教为了让你改造电路,可能会故意出赋值给 rs 寄存器的题)至于为什么是这样,到了我们搭建 CPU 的时候,你自然就会了解了,在这里就先按下不表吧!
下面我们还是举个例子来研究一下。我们来看 ori $s0, $s1, 19 这条指令,如果我告诉你 ori 指令的 OpCode 是 001101 ,你能写出这条指令的机器码吗?
答案是 0x36300013 ,你答对了吗?下面是转换的思路:OpCode 已经给出,是 0b001101 ;接下来是 rs 和 rt ,这里要注意在 ori 指令中,17 号寄存器 $s1 是 rs ,16 号寄存器 $s0 才是 rt ,于是 rs 就是 0b10001 ,而 rt 则是 0b10000 ;最后加上 16 位的立即数 0x0013(这里二进制太长,直接写十六进制了),将上面的所有部分按顺序拼接在一起,就得到了上面的机器码。
【R型指令】
最后就是最复杂,也是最常见的 R 型指令了。你要问我 R 型指令都是啥,我会告诉你,除了 J 型指令和 I 型指令以外,剩下的全都是 R 型指令!
R 型指令更是由惊人的六部分组成。31 到 26 位依旧是 OpCode ,但和前两种指令不一样,R 型指令并不以 OpCode 作为判断依据,我们常用的所有 R 型指令的 OpCode 值全部都是 000000 !真正决定指令种类的是 5 位到 0 位的 Funct ,它们和前两种指令的 OpCode 一样,指示着指令的种类,例如 add 指令的 Funct 为 100000 ,jr 指令的 Funct 为 001000 。
R 型指令中最多可以有三个寄存器,它们分别是 25 到 21 位的 rs ,20 到 16 位的 rt ,以及 15 到 11 位的 rd 。如果哪个寄存器没被用到,相应位全部置 0 即可。于是就有了这种说法:R 型指令不一定要有 3 个寄存器,但有 3 个寄存器的指令一定是 R 型指令!
或许你会发现还有一个部分没有介绍到,那就是存在感最低的(最近几年搭 CPU 时都直接不用考虑的)10 到 6 位的 shamt ,它真的只会用在 sll sra srl 三条指令上,是一个 5 位的立即数,用于表示移位的位数,毕竟移位的位数要 0 到 31 就好。在其它指令中,这 5 位永远都是 00000 。
| 31..26 | 25..21 | 20..16 | 15..11 | 10..6 | 5..0 |
|---|---|---|---|---|---|
| OpCode | rs | rt | rd | shamt | Funct |
和 I 型指令一样,R 型指令各个参数的位置也是千奇百怪,大概可以分为以下几种:
| 指令 | 格式 |
|---|---|
add addu sub subu and or xor nor slt sltu |
add rd, rs, rt |
sll sra srl |
sll rd, rt, shamt |
sllv srav srlv |
sllv rd, rt, rs |
jalr |
jalr rd, rs |
mult multu div divu |
mult rs, rt |
mthi mtlo jr |
mthi rs |
mfhi mflo |
mfhi rd |
syscall break |
syscall |
在 R 型指令中,只要有 rd 寄存器,那么它一定会被赋值,而 rs 和 rt 寄存器均不能被赋值。所以说,rs 寄存器一定不能被赋值,rt 寄存器不一定能不能被赋值,rd 寄存器一定会被赋值。这一点在我们后续设计 CPU 时有很大用处,我们暂且先记住一下。
下面我们就还是浅举两个例子,体会一下 R 型指令的机器码。首先我们来看 add $t0, $t1, $t2 这条指令。刚才我们起到过,add 指令的 Funct 是 100000 ,那么它的机器码是什么呢?
答案是 0x012a4020 。答对了吗?这条指令的 OpCode 是 0b000000 ,shamt 是 0b00000 ,Funct 是 0b100000 。寄存器部分,我们还是不要忘记了寄存器的顺序,按照 add rd, rs, rt 的顺序,排列好寄存器编号:rs 0b01001 ,rt 0b01010 ,rd 0b01000 ,将 6 个部分拼接起来,就能够得到这条指令的机器码了!
再举一个例子吧,观察 sll $t0, $t1, 23 这条指令,已知 sll 指令的 Funct 是 000000 ,那么它的机器码是什么呢?
答案是 0x000945c0 。这回答对了吗?sll 真的是一个很特殊的指令,它的 OpCode 和 Funct 都是 0b000000 。根据上面的顺序表格,可以知道这条指令并没有 rs 寄存器,所以 25 到 21 位为 0b00000 ;rt 寄存器是 $t1 寄存器,所以 20 到 16 位为 0b01001 ;rd 寄存器是 $t0 寄存器,所以 15 到 11 位为 0b01000 ;shamt 位是 23 ,所以 10 到 6 位为 0b10111 。将所有部分合起来即可。
【立即数的扩展】
这里我们简单探讨一下有关立即数扩展的一些小细节。在前面 J 型指令的示例中我们能够看出,机器码中的立即数并不能够直接参与到指令执行中,而是需要进行一些适当的扩展才可以。下面我们就来探讨一下 J 型指令和 I 型指令中立即数的扩展:
对于 j 和 jal 这两条 J 型指令,它们有 26 位的立即数。那么如何用 26 位的立即数表示出 32 位的地址呢?
首先我们能够想到,一条指令在内存中的地址一定是 4 的倍数,所以为了节省位数,我们可以直接舍去 32 位地址的最低两位,因为它们一定是 0 嘛。
现在地址长度变为 30 位了,但是还是没法塞到 26 位的立即数里,该怎么办呢?只能牺牲一下跳转的范围了!于是我们只能砍掉最高的 4 位,选择用当前地址(PC 寄存器的值)的最高 4 位来代替原来的最高 4 位。
(你可能会问,如果要跳转到的地址最高 4 位和当前地址不同,该怎么跳转呢?那就只能用 jr 和 jalr 指令将就一下了~)
于是我们就能够得到 J 型指令中跳转地址的计算方法:将 26 位立即数左移 2 位,并在高位处拼接当前地址的最高 4 位。
接下来是 I 型指令,I 型指令中的 16 位立即数又是怎么被解释成 32 位的呢?我们来分类讨论一下:
对于 i 家族的指令和内存访存指令,这个问题就比较简单了。我们只需要将 16 位立即数直接扩展到 32 位即可。当然,位扩展就一定要考虑到有无符号扩展的问题。这里就直接说结论了,在 MIPS 中,只有位运算的指令 andi ori xori 是无符号扩展,其余所有的指令对 16 位立即数都是有符号扩展(哪怕是名称里面带 u 也是!)
实际上相对跳转指令也是一样的道理,只不过在将相对条数转换为跳转地址时需要再花一步。对 16 位立即数符号扩展到 32 位,就已经得到了我们之前提到的相对条数。之后我们需要将相对条数左移 2 位,再与当前指令的下一条指令的地址(PC + 4)相加,才能够得到我们要跳转的真实地址。
【使用符号语言描述指令功能】
在本章的结尾,我们来简单了解一下如何使用符号语言来描述一条指令的功能,毕竟如果每条指令都用语言描述的话,可能很难准确地表述出来。有了符号语言之后,我们就可以快速地了解到一条指令的作用,以及它的底层逻辑了!
下面我们来认识一些基本的符号。GPR[num] 表示编号 num 对应的寄存器,Memory[addr] 则表示内存中以 addr 为首地址的一个字(4 字节)。左箭头 ← 代表赋值,双竖线 || 代表位拼接,上角标 $ 0^{32} $ 代表重复次数,下角标 $ temp_{31} $ 代表取相应位数,当取多个连续位时可以用两个点省略写作 $ temp_{15..0} $ 。zero_extend() 表示无符号扩展,sign_extend() 表示有符号扩展。结合一些 C 语言中常用的符号,我们就能够使用符号化的语言描述指令的功能了!
下面我们来举几个例子,直观感受一下符号语言描述的强度。首先是 sb 指令,它的符号语言是这样的:
Addr ← GPR[base] + sign_extend(offset) byte ← Addr1..0 memory[Addr]7+8*byte..8*byte ← GPR[rt]7:0








.png)
.png)
.png)
.png)


.png)